题目内容
甲袋中装有大小相同的红球1个,白球2个;乙袋中装有与甲袋中相同大小的红球2个,白球3个.先从甲袋中取出1个球投入乙袋中,然后从乙袋中取出2个小球.
(Ⅰ)求从乙袋中取出的2个小球中仅有1个红球的概率;
(Ⅱ)记从乙袋中取出的2个小球中白球个数为随机变量 ,求
,求 的分布列和数学期望.
的分布列和数学期望.
(Ⅰ)求从乙袋中取出的2个小球中仅有1个红球的概率;
(Ⅱ)记从乙袋中取出的2个小球中白球个数为随机变量
 ,求
,求 的分布列和数学期望.
的分布列和数学期望.(Ⅰ)记“乙袋中取出的2个小球中仅有1个红球”为事件A,包含如下两个事件:“从甲袋中取出1红球投入乙袋,然后从乙袋取出的两球中仅1个红球”、“从甲袋中取出1白球投入乙袋,然后从乙袋取出的两球中仅1个红球”,分别记为事件A1、A2,且A1与A2互斥,则: ,
, ,·· 4分
,·· 4分
∴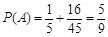 ,
,
故从乙袋中取出的2个小球中仅有1个红球的概率为 .············ 6分
.············ 6分
(Ⅱ) =0、1、2.
=0、1、2.
 ,
, ,
,
 ,(答对一个得1分)··············· 9分
,(答对一个得1分)··············· 9分
∴ 的分布列为
的分布列为
∴ .(分布列1分,方差2分;分布列部分对给1分)
.(分布列1分,方差2分;分布列部分对给1分)
 ,
, ,·· 4分
,·· 4分∴
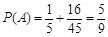 ,
,故从乙袋中取出的2个小球中仅有1个红球的概率为
 .············ 6分
.············ 6分(Ⅱ)
 =0、1、2.
=0、1、2. ,
, ,
, ,(答对一个得1分)··············· 9分
,(答对一个得1分)··············· 9分∴
 的分布列为
的分布列为 | 0 | 1 | 2 |
| P |  |  |  |
 .(分布列1分,方差2分;分布列部分对给1分)
.(分布列1分,方差2分;分布列部分对给1分)略

练习册系列答案
相关题目
 且互相独立,灯亮的概率为 ( )。
且互相独立,灯亮的概率为 ( )。 




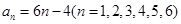 构成集合
构成集合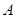 ,
,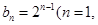
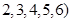 构成集合
构成集合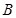 ,任取
,任取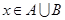 ,则
,则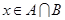 的概率是_______.
的概率是_______.