题目内容
将一颗骰子投掷两次分别得到点数a,b,则直线ax-by=0与圆(x-2)2+y2=2相交的概率为 .
5/12
解:∵直线ax-by=0与圆(x-2)2+y2=2相交,∴圆心到直线的距离|2a|/a2+b2<2即a<b
∵设一颗骰子投掷两次分别得到点数为(a,b),则这样的有序整数对共有6×6=36个
其中a<b的有(1,2),(1,3),(1,4),(1,5),(1,6),(2,3),(2,4),(2,5),(2,6),(3,4),(3,5),(3,6),(4,5),(4,6),(5,6)共5+4+3+2+1=15个
∴直线ax-by=0与圆(x-2)2+y2=2相交的概率为P=15/36=5/12
∵设一颗骰子投掷两次分别得到点数为(a,b),则这样的有序整数对共有6×6=36个
其中a<b的有(1,2),(1,3),(1,4),(1,5),(1,6),(2,3),(2,4),(2,5),(2,6),(3,4),(3,5),(3,6),(4,5),(4,6),(5,6)共5+4+3+2+1=15个
∴直线ax-by=0与圆(x-2)2+y2=2相交的概率为P=15/36=5/12

练习册系列答案
相关题目
 ,
, ,
, 三个兴趣小组,为了对兴趣小组活动的开展情况进行调查,用分层抽样方法从
三个兴趣小组,为了对兴趣小组活动的开展情况进行调查,用分层抽样方法从

 ,从集合{1,2,3}中随机抽取一个数为
,从集合{1,2,3}中随机抽取一个数为 ,则
,则 的概率是( )
的概率是( ) 



 ,求
,求



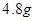 的概率为
的概率为 ,质量小于
,质量小于 的概率为
的概率为 ,那么质量在
,那么质量在 (
( )范围内的概率是( )
)范围内的概率是( )



 ,又
,又 (A)表示集合的元素个数,A={
(A)表示集合的元素个数,A={ |
|


