题目内容
用演绎法证明函数 是增函数时的小前提是
是增函数时的小前提是
| A.增函数的定义 |
B.函数 满足增函数的定义 满足增函数的定义 |
C.若 ,则 ,则 |
D.若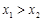 ,则 ,则 |
B
解析试题分析:∵证明y=x3是增函数时,依据的原理就是增函数的定义,∴用演绎法证明y=x3是增函数时的大前提是:增函数的定义,小前提是函数f(x)=x3满足增函数的定义.故选B.
考点:演绎推理的基本方法.

练习册系列答案
相关题目
观察按下列顺序排列的等式: ,
, ,
, ,
, ,…,猜想第
,…,猜想第 个等式应为( )
个等式应为( )
A. | B. |
C. | D. |
凡自然数都是整数,而 4是自然数 所以,4是整数。以上三段论推理( )
| A.正确 | B.推理形式不正确 |
| C.两个“自然数”概念不一致 | D.两个“整数”概念不一致 |
演绎推理“因为对数函数 是增函数,而函数
是增函数,而函数 是对数函数,所以
是对数函数,所以 是增函数”所得结论错误的原因是( )
是增函数”所得结论错误的原因是( )
| A.大前提错误 | B.小前提错误 |
| C.推理形式错误 | D.大前提和小前提都错误 |
要证明 ,可选择的方法有以下几种,其中最合理的是( )
,可选择的方法有以下几种,其中最合理的是( )
| A.综合法 | B.分析法 | C.反证法 | D.归纳法 |
用反证法证明命题“若实系数一元二次方程 有有理根,那么
有有理根,那么 中至少有一个是偶数”时,下列假设正确的是( )
中至少有一个是偶数”时,下列假设正确的是( )
A.假设 都是偶数 都是偶数 | B.假设 都不是偶数 都不是偶数 |
C.假设 至多有一个是偶数 至多有一个是偶数 | D.假设 至少有两个是偶数 至少有两个是偶数 |
用数学归纳法证明1+2+3+…+n2= ,则当n=k+1时左端应在n=k的基础上加上( )
,则当n=k+1时左端应在n=k的基础上加上( )
| A.k2+1 |
| B.(k+1)2 |
C. |
| D.(k2+1)+(k2+2)+…+(k+1)2 |
设a,b是两个实数,给出下列条件:
①a+b>1;②a+b=2;③a+b>2;④a2+b2>2;⑤ab>1.
其中能推出:“a,b中至少有一个大于1”的条件是( )
| A.②③ | B.①②③ | C.③ | D.③④⑤ |
 的值依次为
的值依次为 ,其中
,其中 且
且 .
. ,写出全部输出结果.
,写出全部输出结果. ,记
,记 ,求
,求 与
与 的关系(
的关系(