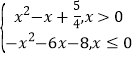题目内容
【题目】己知函数![]()
(1)设![]() 时,判断函数
时,判断函数![]() 在
在![]() 上的零点的个数;
上的零点的个数;
(2)当![]() ,是否存在实数
,是否存在实数![]() ,对
,对![]() 且
且![]() ,有
,有![]() 恒成立,若存在,求出
恒成立,若存在,求出![]() 的范围:若不存在,请说明理由.
的范围:若不存在,请说明理由.
【答案】(1)![]() 在
在![]() 上无零点(2)存在,
上无零点(2)存在,![]() 的取值范围是[2,+∞)
的取值范围是[2,+∞)
【解析】
(1)利用导数可知函数![]() 在(0,1),(1,+∞)单调递增,在(1,
在(0,1),(1,+∞)单调递增,在(1,![]() )上递减,可得
)上递减,可得![]() 在
在![]() 单调递增且
单调递增且![]() 可知无零点(2)化简得
可知无零点(2)化简得![]() ,由
,由![]() 可得
可得![]() (
(![]() )恒成立,构造函数
)恒成立,构造函数![]() ,需有
,需有![]() 恒成立,分离参数求解即可.
恒成立,分离参数求解即可.
(1)![]() 的定义域是(0,+∞)
的定义域是(0,+∞)
![]() ,
,![]()
令![]() 得到:
得到:![]() ,
,![]() ,且
,且![]()
所以函数![]() 在(0,1),(1,+∞)单调递增,在(1,
在(0,1),(1,+∞)单调递增,在(1,![]() )上递减
)上递减
因为![]()
所以![]() 在
在![]() 单调递增,
单调递增,
因为![]() ,
,
所以![]() 在
在![]() 上无零点.
上无零点.
(2)因为![]() ,
,
所以![]()
化简得![]()
不妨设![]() 可化为
可化为![]() ;
;
考查函数![]() 则
则![]()
即![]() ,整理可得
,整理可得![]()
令![]() ,则
,则![]() ,
,
因此![]() 单调递減,所以
单调递減,所以![]()
所以![]()
综上:![]() 的取值范围是[2,+∞)
的取值范围是[2,+∞)

练习册系列答案
 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
【题目】通过随机询问100名性别不同的大学生是否爱好某项运动,得到如下![]() 列联表:
列联表:
(1)能否有![]() 的把握认为是否爱好该项运动与性别有关?请说明理由.
的把握认为是否爱好该项运动与性别有关?请说明理由.
(2)利用分层抽样的方法从以上爱好该项运动的大学生中抽取6人组建“运动达人社”,现从“运动达人社”中选派2人参加某项校际挑战赛,求选出的2人中恰有1名女大学生的概率.
男 | 女 | 总计 | |
爱好 | 40 | 20 | 60 |
不爱好 | 15 | 25 | 40 |
总计 | 55 | 45 | 100 |
附:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
 ,其中
,其中![]()