题目内容

如图，直三棱柱ABC—A1B1C1，底面△ABC中，CA=CB=1，∠BCA=90°，棱AA1=2，M、N分别是A1B1、A1A的中点.

(1)求的长；?

(2)求cos〈,〉的值.

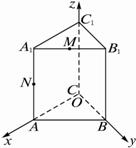
解析：以C为原点，以、、的方向为x轴、y轴、z轴的正方向，建立空间直角坐标系C—xyz.

(1)依题意得B(0,1,0),N(1,0,1),?

∴|BN|==.

(2)依题意得A1(1,0,2),B(0,1,0),C(0,0,0),B1(0,1,2).?

∴=(1,-1,2), =(0,1,2), ·=3.

∴||=,| |=.

∴cos〈,〉==.

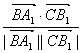温馨提示：建立恰当的空间直角坐标系，运用向量的坐标运算求夹角与距离是一种重要的方法，同学们务必要学会.

练习册系列答案
相关题目
精英家教网如图，直三棱柱ABC-A1B1C1中，∠ACB=90°，AC=1，CB=
2
，侧棱AA1=1，侧面AA1B1B的两条对角线交于点D，B1C1的中点为M，求证：CD⊥平面BDM．
精英家教网如图，直三棱柱ABC-A1B1C1中，底面是以∠ABC为直角的等腰直角三角形，AC=2a，BB1=3a，D为A1C1的中点，E为B1C的中点．
（1）求直线BE与A1C所成的角；
（2）在线段AA1中上是否存在点F，使CF⊥平面B1DF，若存在，求出|
AF
|；若不存在，说明理由．
精英家教网如图在直三棱柱ABC-A1B1C1中∠ACB=90°，AA1=2，AC=BC=1，则异面直线A1B与AC所成角的余弦值是
 
．
如图，直三棱柱ABC-A1B1C1中，AC⊥BC，AC=BC=CC1=2，M，N分别为AC，B1C1的中点．
（Ⅰ）求线段MN的长；
（Ⅱ）求证：MN∥平面ABB1A1；
（Ⅲ）线段CC1上是否存在点Q，使A1B⊥平面MNQ？说明理由．
精英家教网如图，直三棱柱ABC-A1B1C1中，∠BAC=90°，AB=AC=a，AA1=2a，D棱B1B的中点．
（Ⅰ）证明：A1C1∥平面ACD；
（Ⅱ）求异面直线AC与A1D所成角的大小；
（Ⅲ）证明：直线A1D⊥平面ADC．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网