题目内容
15.已知定义在R上的函数f(x)=$\frac{b-{2}^{x}}{{2}^{x}+a}$是奇函数(1)求a,b的值;
(2)判断f(x)的单调性,并用单调性定义证明;
(3)若对任意的t∈(-∞,1],不等式f(1+2t)+f(k•4t)<0恒成立,求实数k的取值范围.
分析 (1)利用奇函数的定义将问题转化为恒成立问题,利用对应系数相等获得解答,
(2)先在定义域上取值,再作差、变形,变形彻底后根据式子的特点,讨论判断符号、下结论;
(3)对任意的t∈(-∞,1],不等式f(1+2t)+f(k•4t)<0恒成立,得-k•4t<(1+2t),-k<{$\frac{1}{{4}^{t}}$+$\frac{1}{{2}^{t}}$}min,t∈(-∞,1],即可获得解答.
解答 解:(1)∵定义在R上的函数f(x)=$\frac{b-{2}^{x}}{{2}^{x}+a}$是奇函数,
∴f(-x)=$\frac{b-{2}^{-x}}{{2}^{-x}+a}$=-$\frac{b-{2}^{x}}{{2}^{x}+a}$,
∴b=1,a=1;
(2)f(x)=$\frac{1-{2}^{x}}{{2}^{x}+1}$=-1+$\frac{2}{{2}^{x}+1}$在R上是单调减函数.
设0<x1<x2,则有f(x1)-f(x2)=-1+$\frac{2}{{2}^{{x}_{1}}+1}$+1-$\frac{2}{{2}^{{x}_{2}}+1}$=$\frac{2({2}^{{x}_{2}}-{2}^{{x}_{1}})}{({2}^{{x}_{1}}+1)({2}^{{x}_{2}}+1)}$
∵0<x1<x2,
∴f(x1)-f(x)>0,即f(x1)>f(x2)
∴函数f(x)=$\frac{1-{2}^{x}}{{2}^{x}+1}$在区间(0,+∞)上是单调递减函数,
∵函数是奇函数,
∴f(x)=$\frac{1-{2}^{x}}{{2}^{x}+1}$在R上是单调减函数.
(3)函数y=f(x)为奇函数且在R上为减函数
由对任意的t∈(-∞,1],不等式f(1+2t)+f(k•4t)<0恒成立,
得-k•4t<(1+2t),
∴-k<$\frac{1}{{4}^{t}}$+$\frac{1}{{2}^{t}}$对一切t∈(-∞,1]恒成立
∴-k<{$\frac{1}{{4}^{t}}$+$\frac{1}{{2}^{t}}$}min,t∈(-∞,1],
∴-k<$\frac{3}{4}$,
∴k>-$\frac{3}{4}$.
点评 本题考查的是函数的奇偶性和单调性问题.在解答的过程当中充分体现了恒成立思想.函数单调性的证明方法:定义法,关键是变形一定彻底,直到能明显的判断出符号为止.

 星级口算天天练系列答案
星级口算天天练系列答案| 销售单价/元 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 日均销售量/桶 | 360 | 320 | 280 | 240 | 200 | 160 | 120 |
| A. | log2[(-3)(-5)]=log2(-3)+log2(-5) | B. | log2(-10)2=2log2(-10) | ||
| C. | log2[(-3)(-5)]=log23+log25 | D. | log2(-5)3=-log253 |
| A. | 7π | B. | 14π | C. | $\frac{7}{2}π$ | D. | $\frac{{7\sqrt{14}π}}{3}$ |
 已知函数f(x)=logax(a>0,a≠1)
已知函数f(x)=logax(a>0,a≠1)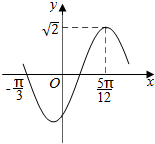 函数f(x)=$\sqrt{2}$sin(ωx+φ)(x∈R,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则f(x)的解析式为f(x)=$\sqrt{2}$sin(2x+$\frac{π}{6}$);f(x)的图象的横坐标缩小为原来的$\frac{1}{2}$后得函数y=g(x)的图象,则g(x)的单调减区间为[$\frac{π}{12}$+$\frac{1}{2}$kπ,$\frac{π}{3}$+$\frac{1}{2}$kπ],k∈Z.
函数f(x)=$\sqrt{2}$sin(ωx+φ)(x∈R,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则f(x)的解析式为f(x)=$\sqrt{2}$sin(2x+$\frac{π}{6}$);f(x)的图象的横坐标缩小为原来的$\frac{1}{2}$后得函数y=g(x)的图象,则g(x)的单调减区间为[$\frac{π}{12}$+$\frac{1}{2}$kπ,$\frac{π}{3}$+$\frac{1}{2}$kπ],k∈Z.