题目内容
符号[x]表示不超过x的最大整数,如[2]=2,[π]=3,[-
]=-2,定义函数f(x)=x-[x].设函数g(x)=-
,若f(x)在区间x∈(0,2)上零点的个数记为a,f(x)与g(x)图象交点的个数记为b,则
g(x)dx的值是( )
| 2 |
| x |
| 3 |
| ∫ | b a |
| A、-2 | ||
B、-
| ||
C、-
| ||
D、-
|
分析:先画出f(x)=x-[x]的图象,根据图象求出a和b的值得到积分上下限,再根据定积分的运算法则求出所求即可.
解答: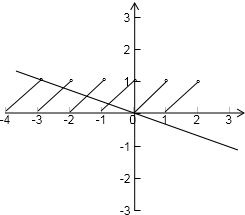 解:画出函数f(x)=x-[x]的图象.
解:画出函数f(x)=x-[x]的图象.
由图象可知若f(x)在区间x∈(0,2)上零点的个数记为a=1,f(x)与g(x)图象交点的个数记为b=4
g(x)dx=∫14(-
)dx=(-
)|14=-
,
故选D.
 解:画出函数f(x)=x-[x]的图象.
解:画出函数f(x)=x-[x]的图象.由图象可知若f(x)在区间x∈(0,2)上零点的个数记为a=1,f(x)与g(x)图象交点的个数记为b=4
| ∫ | b a |
| x |
| 3 |
| x2 |
| 6 |
| 5 |
| 2 |
故选D.
点评:本题主要考查了定积分的运算,定积分是一种“和”的极限,蕴含着分割、近似代替,求和、取极限的思想方法,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目