题目内容
17.已知直线l与曲线$y=-\frac{1}{x}$和曲线y=lnx均相切,则这样的直线l的条数为1.分析 设出两切点(m,n),(s,t),求出导数,由两点的斜率公式,可有$\frac{1}{{m}^{2}}$=$\frac{1}{s}$=$\frac{n-t}{m-s}$=$\frac{\frac{-1}{m}-lns}{m-s}$,化简整理可得即为$\frac{1}{2}$+$\frac{1}{-m}$=ln(-m),(m<0),令x=-m,则有lnx=$\frac{1}{2}$+$\frac{1}{x}$,令f(x)=lnx-$\frac{1}{2}$-$\frac{1}{x}$,运用零点存在定理,即可判断零点个数,进而得到公切线条数.
解答 解:设与曲线y=-$\frac{1}{x}$(x<0)和曲线y=lnx相切的切点分别为(m,n),(s,t),
则n=-$\frac{1}{m}$,t=lns,(m<0,s>0),
由(-$\frac{1}{x}$)′=$\frac{1}{{x}^{2}}$,(lnx)′=$\frac{1}{x}$,
即有$\frac{1}{{m}^{2}}$=$\frac{1}{s}$=$\frac{n-t}{m-s}$=$\frac{\frac{-1}{m}-lns}{m-s}$,
即m2=s,1-m=-1-mlns,
即为$\frac{1}{2}$+$\frac{1}{-m}$=ln(-m),(m<0),
令x=-m,则有lnx=$\frac{1}{2}$+$\frac{1}{x}$,
令f(x)=lnx-$\frac{1}{2}$-$\frac{1}{x}$,
f′(x)=$\frac{1}{x}$+$\frac{1}{{x}^{2}}$>0,f(x)递增,
f(2)=ln2-1<0,f(3)=ln3-$\frac{5}{6}$>0,
由零点存在定理可得f(x)=0有且只有一个实根,
即有m唯一,s唯一,
则有公切线的条数为1.
故答案为:1.
点评 本题考查导数的几何意义:函数在某点处的导数即为曲线在该点处的切线斜率,运用两点的斜率公式和零点存在定理是解题的关键.

 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案| A. | $\frac{{\sqrt{3}}}{24}π$ | B. | $\frac{{\sqrt{3}}}{8}π$ | C. | $\frac{1}{16}π$ | D. | $\frac{1}{8}π$ |
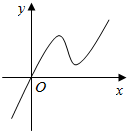 已知函数f(x)的定义域为R,且满足f(4)=1,f′(x)为f(x)的导函数,又知y=f′(x)的图象如图所示,若两个正数a,b满足,f(2a+b)<1,则$\frac{b+2}{a+1}$的取值范围是( )
已知函数f(x)的定义域为R,且满足f(4)=1,f′(x)为f(x)的导函数,又知y=f′(x)的图象如图所示,若两个正数a,b满足,f(2a+b)<1,则$\frac{b+2}{a+1}$的取值范围是( )| A. | $({\frac{2}{3},6})$ | B. | $[{\frac{2}{3},6}]$ | C. | $[\frac{1}{4},\frac{5}{2}]$ | D. | $({\frac{1}{4},\frac{5}{2}})$ |
| A. | {4} | B. | {3,4} | C. | {2,3,4} | D. | {1,2,3,4} |
| A. | (-1,$\frac{2}{3}$] | B. | (-1,$\frac{2}{3}$) | C. | (-∞,-1)∪(-1,$\frac{2}{3}$] | D. | [$\frac{2}{3}$,+∞) |
| A. | 递增数列 | B. | 递减数列 | ||
| C. | 常数列 | D. | 递增数列或递减数列都有可能 |
 在正方体ABCD-A1B1C1D1中,G是C1D1的中点,H是A1B1的中点
在正方体ABCD-A1B1C1D1中,G是C1D1的中点,H是A1B1的中点