题目内容
设集合P={-2,-1,0,1,2},x∈P且y∈P,则点(x,y)在圆x2+y2=4内部的概率为
.
| 9 |
| 25 |
| 9 |
| 25 |
分析:本题考查的知识点是古典概型,我们要计算出满足:“x∈P且y∈P”,代表的点(x,y)的总的事件总个数,及点(x,y)在圆x2+y2=4内部的基本事件个数,然后代入古典概型公式即可求解.
解答: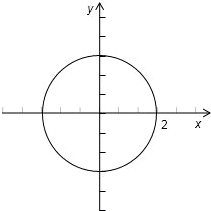 解:设集合P={-2,-1,0,1,2},x∈P且y∈P,代表的点(x,y)共有:
解:设集合P={-2,-1,0,1,2},x∈P且y∈P,代表的点(x,y)共有:
5×5,共25种情况,
其中点(x,y)落在圆x2+y2=4内部的基本事件个数有:
(-1,1),(-1,0),(1,1),
(-1,0),(0,0),(1,0),
(-1,-1),(0,-1),(1,-1),共9种情况,
故点(x,y)落在圆x2+y2=4内部的概率P=
故答案为
.
 解:设集合P={-2,-1,0,1,2},x∈P且y∈P,代表的点(x,y)共有:
解:设集合P={-2,-1,0,1,2},x∈P且y∈P,代表的点(x,y)共有:5×5,共25种情况,
其中点(x,y)落在圆x2+y2=4内部的基本事件个数有:
(-1,1),(-1,0),(1,1),
(-1,0),(0,0),(1,0),
(-1,-1),(0,-1),(1,-1),共9种情况,
故点(x,y)落在圆x2+y2=4内部的概率P=
| 9 |
| 25 |
故答案为
| 9 |
| 25 |
点评:本古典概型要求所有结果出现的可能性都相等,强调所有结果中每一结果出现的概率都相同.弄清一次试验的意义以及每个基本事件的含义是解决问题的前提,正确把握各个事件的相互关系是解决问题的关键.解决问题的步骤是:计算满足条件的基本事件个数,及基本事件的总个数,然后代入古典概型计算公式进行求解.

练习册系列答案
相关题目