题目内容
| |||||||||||||||
解析:
(1) |
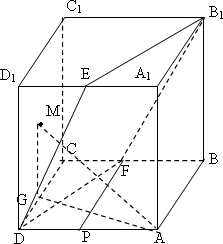
证明:连接AM,过M作MG⊥CD于G,连接AG ∵正方体ABCD-A1B1C1D1,MG⊥CD∴MG⊥平面ABCD 又∵M为正方形DCC1D1的中心,MG⊥CD∴G为CD中点 在正方形ABCD中,F为CB中点∴CF=DG 又∵AD=DC∠DCF=∠ADG=Rt∠AMG ∴△ADG≌△DCF∴∠AGD=∠DFC ∴AG⊥DF 由MG⊥平面ABCD,AG⊥DF可得AM⊥DF,同理可得AM⊥DE ∴AM⊥平面B1FDE----------------------4分 |
(2) |
设A到平面DEB1F的距离为 ∵E到平面ADF的距离为 ∴ 又∵ 而 |
(3) |
过F作FP⊥AD于P,过P作PQ⊥DE于Q,连接FQ ∵FP⊥平面DEP,PQ⊥DE ∴FQ⊥DE ∴∠FQP为二面角A-DE-F的平面角-----------------------------------11分 ∵ ∴ 在Rt△FPQ中 ∴二面角A-DE-F的大小为 |

| |||||||||||
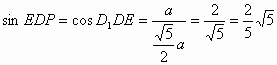
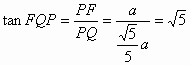 --------------------13分
--------------------13分