Question

【题目】已知数列{an}满足： ，anan+1＜0（n≥1），数列{bn}满足：bn=an+12﹣an2（n≥1）． （Ⅰ）求数列{an}，{bn}的通项公式
（Ⅱ）证明：数列{bn}中的任意三项不可能成等差数列．

Answer 1

【答案】解：（Ⅰ）由题意可知，

令cn=1﹣an2，则

又 ，则数列{cn}是首项为 ，公比为 的等比数列，即 ，

故 ，

又 ，anan+1＜0

故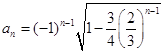

因为 = ，

故

（Ⅱ）假设数列{bn}存在三项br，bs，bt（r＜s＜t）按某种顺序成等差数列，

由于数列{bn}是首项为 ，公比为 的等比数列，

于是有2bs=br+bt成立，则只有可能有2br=bs+bt成立，

∴

化简整理后可得，2=（ ）r﹣s+（ ）t﹣s，

由于r＜s＜t，且为整数，故上式不可能成立，导致矛盾．

故数列{bn}中任意三项不可能成等差数列．

【解析】（1）对 化简整理得 ，令cn=1﹣an2，进而可推断数列{cn}是首项为 ，公比为 的等比数列，根据等比数列通项公式求得cn，则a2n可得，进而根据anan+1＜0求得an．（2）假设数列{bn}存在三项br，bs，bt（r＜s＜t）按某种顺序成等差数列，由于数列{bn}为等比数列，于是有br＞bs＞bt，则只有可能有2bs=br+bt成立，代入通项公式，化简整理后发现等式左边为2，右边为分数，故上式不可能成立，导致矛盾．
【考点精析】掌握数列的定义和表示和等差数列的性质是解答本题的根本，需要知道数列中的每个数都叫这个数列的项．记作an，在数列第一个位置的项叫第1项（或首项），在第二个位置的叫第2项，……，序号为n的项叫第n项（也叫通项）记作an；在等差数列{an}中，从第2项起，每一项是它相邻二项的等差中项；相隔等距离的项组成的数列是等差数列．