题目内容
已知对一组观测值(xi,yi)(i=1,2,…,n)作出散点图后,确定具有线性相关关系,若对于 =
= +
+ x,求得
x,求得 =0.51,
=0.51, =61.75,
=61.75, =38.14,则线性回归方程为________.
=38.14,则线性回归方程为________.
 =
= +
+ x,求得
x,求得 =0.51,
=0.51, =61.75,
=61.75, =38.14,则线性回归方程为________.
=38.14,则线性回归方程为________. =0.51x+6.65
=0.51x+6.65∵ =
= -
-
 =38.14-0.51×61.75=6.647 5≈6.65.
=38.14-0.51×61.75=6.647 5≈6.65.
∴ =0.51x+6.65.
=0.51x+6.65.
 =
= -
-
 =38.14-0.51×61.75=6.647 5≈6.65.
=38.14-0.51×61.75=6.647 5≈6.65.∴
 =0.51x+6.65.
=0.51x+6.65.
练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
 、
、 两种元件,其质量按测试指标划分为:大于或等于
两种元件,其质量按测试指标划分为:大于或等于 为正品,小于
为正品,小于 件进行检测,检测结果记录如下:
件进行检测,检测结果记录如下:






 ,且
,且 件,求
件,求
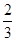

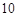 分钟从中抽取一件产品进行某项指标检测,这样的抽样是分层抽样;
分钟从中抽取一件产品进行某项指标检测,这样的抽样是分层抽样;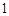 ;
;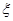 服从正态分布
服从正态分布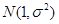
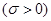 ,若
,若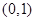 内的概率为
内的概率为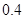 ,则
,则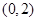 内的概率为
内的概率为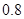 ;
;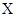 与
与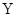 的随机变量K2的观测值k来说,k越小,判断“
的随机变量K2的观测值k来说,k越小,判断“