题目内容
某工厂生产 、
、 两种元件,其质量按测试指标划分为:大于或等于
两种元件,其质量按测试指标划分为:大于或等于 为正品,小于
为正品,小于 为次品.现从一批产品中随机抽取这两种元件各
为次品.现从一批产品中随机抽取这两种元件各 件进行检测,检测结果记录如下:
件进行检测,检测结果记录如下:
由于表格被污损,数据 、
、 看不清,统计员只记得
看不清,统计员只记得 ,且
,且 、
、 两种元件的检测数据的平均值相等,方差也相等.
两种元件的检测数据的平均值相等,方差也相等.
(1)求表格中 与
与 的值;
的值;
(2)从被检测的 件
件 种元件中任取
种元件中任取 件,求
件,求 件都为正品的概率.
件都为正品的概率.
 、
、 两种元件,其质量按测试指标划分为:大于或等于
两种元件,其质量按测试指标划分为:大于或等于 为正品,小于
为正品,小于 为次品.现从一批产品中随机抽取这两种元件各
为次品.现从一批产品中随机抽取这两种元件各 件进行检测,检测结果记录如下:
件进行检测,检测结果记录如下: |  |  |  |  |  |
| B |  |  |  |  |  |
 、
、 看不清,统计员只记得
看不清,统计员只记得 ,且
,且 、
、 两种元件的检测数据的平均值相等,方差也相等.
两种元件的检测数据的平均值相等,方差也相等.(1)求表格中
 与
与 的值;
的值;(2)从被检测的
 件
件 种元件中任取
种元件中任取 件,求
件,求 件都为正品的概率.
件都为正品的概率.(1)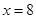 ,
, ;(2)
;(2)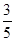 .
.
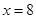 ,
, ;(2)
;(2)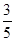 .
.试题分析:(1)根据
 、
、 两种元件的检测数据的平均数与方差分别相等,利用平均数与方差的计算公式列方程组求出
两种元件的检测数据的平均数与方差分别相等,利用平均数与方差的计算公式列方程组求出 与
与 的值;(2)将
的值;(2)将 件
件 元件编号,并将说明哪些是正品,利用列举法将所有的基本事件与问题中涉及事件所包含的基本进行列举,然后利用古典概型的概率计算公式求出相应事件的概率.
元件编号,并将说明哪些是正品,利用列举法将所有的基本事件与问题中涉及事件所包含的基本进行列举,然后利用古典概型的概率计算公式求出相应事件的概率.试题解析:(1)因为
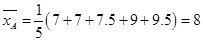 ,
,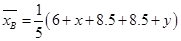 ,
,由
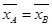 ,得
,得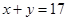 ,①
,①因为
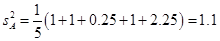 ,
,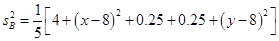 ,
,由
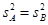 ,得
,得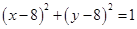 ,②
,②由①②解得
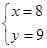 或
或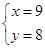 ,
,因为
 ,所以
,所以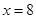 ,
, ;
;(2)记被检测的
 件的
件的 种元件分别为
种元件分别为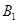 、
、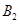 、
、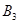 、
、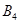 、
、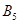 ,其中
,其中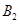 、
、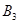 、
、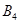 、
、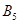 为正品,
为正品,从中任取
 件,共有
件,共有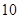 个基本事件,列举如下:
个基本事件,列举如下: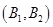 、
、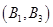 、
、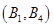 、
、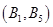 、
、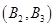 、
、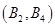 、
、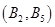 、
、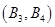 、
、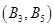 、
、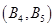 ,
,记“
 件都为正品”为事件
件都为正品”为事件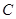 ,则事件
,则事件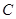 包含以下
包含以下 个基本事件:
个基本事件: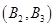 、
、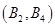 、
、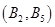 、
、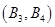 、
、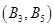 、
、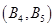 ,
,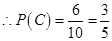 ,所以
,所以 件都为正品的概率为
件都为正品的概率为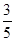 .
.
练习册系列答案
相关题目
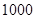 人,其中
人,其中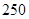 名工人参加过短期培训(称为
名工人参加过短期培训(称为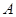 类工人),另外
类工人),另外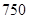 名工人参加过长期培训(称为
名工人参加过长期培训(称为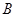 类工人).现用分层抽样的方法(按
类工人).现用分层抽样的方法(按 名工人,调查他们的生产能力(此处的生产能力指一天加工的零件数).
名工人,调查他们的生产能力(此处的生产能力指一天加工的零件数).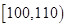
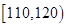
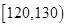
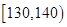
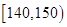
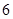
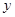
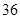
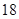
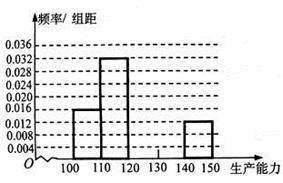
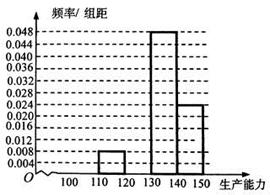
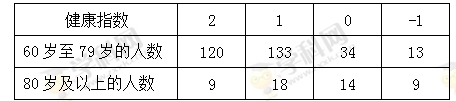
 五个等级. 某考场考生的两科考试成绩数据统计如下图所示,其中“数学与逻辑”科目的成绩为
五个等级. 某考场考生的两科考试成绩数据统计如下图所示,其中“数学与逻辑”科目的成绩为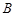 的考生有
的考生有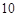 人.
人. 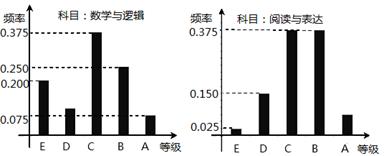
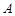 的人数;
的人数; 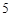 分,
分,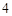 分,
分,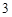 分,
分,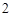 分,
分, 分,求该考场考生“数学与逻辑”科目的平均分;
分,求该考场考生“数学与逻辑”科目的平均分;  =
= +
+ x,求得
x,求得 =61.75,
=61.75, =38.14,则线性回归方程为________.
=38.14,则线性回归方程为________. 三种个体按
三种个体按 的比例分层抽样调查,如果抽取的
的比例分层抽样调查,如果抽取的 个体为9个,则样本容量为30;
个体为9个,则样本容量为30; ,则
,则 每增加1个单位,
每增加1个单位, 平均减少2个单位;
平均减少2个单位; 内的频率为0.4.
内的频率为0.4.