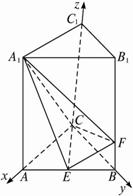
题目内容
如图,在直三棱柱ABC—A1B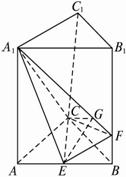
(1)求二面角C-A
(2)求点E到平面CA
解法一:(1)过E作EG⊥FA1,垂足为G,连结CG.?
在直三棱柱ABC—A1B
又AC=BC,E为AB中点,?
∴CE⊥AB.∴CE⊥面A1B.?
∴CG⊥A
∴∠CGE为二面角CA1FE的平面角. ?
又∵CE⊥面A1B,?
∴CE⊥EF.?
而EF⊥CA1,∴EF⊥面A1CE.∴EF⊥A1E. ?
∴△A1AE∽△EBF.?
∴BF= .?
.?
在RT△A1AE中,A1E=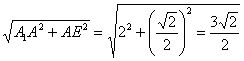 .?在RT△EBF中,EF=
.?在RT△EBF中,EF= ,
,
∴A![]() .?
.?
∴EG= . ?
. ?
又CE=![]() ,?
,?
∴tan∠CGE=![]() =1.∴∠CGE=45°, ?
=1.∴∠CGE=45°, ?
即二面角CA1FE的大小为45°.?
(2)设顶点E到平面A1CF的距离为d,?
由(1)CG=1,CE⊥面A1B,A
VE—A1CF=VC—A1EF,?
∴![]() CE·
CE·![]() A1E·EF=
A1E·EF=![]() ×
×![]() ·CG·A
·CG·A
∴![]() .?
.?
∴d=![]() ,
,
即点E到平面CA![]() . ?
. ?

解法二:(1)如图,分别以CA、CB、CC1为x轴、y轴、z轴建立空间直角坐标系,并设BF=x,则C(0,0,0),A(1,0,0),B(0,1,0),E(![]() ,
,![]() ,0),F(0,1,x),A1(1,0,2),则
,0),F(0,1,x),A1(1,0,2),则![]() =(-
=(-![]() ,
,![]() ,x),
,x),![]() =(1,0,2).?
=(1,0,2).?
∵EF⊥CA1,则![]() ·
·![]() =0,?
=0,?
∴-![]() ×1+
×1+![]() ×0+2x=0,?
×0+2x=0,?
x=![]() .∴F(0,1,
.∴F(0,1, ![]() ). ?
). ?
设向量n=(x,y,z)为平面A1CF的法向量,则n·![]() =0,
=0,
n·![]() =0.?
=0.?
又![]() =(1,0,2),
=(1,0,2), ![]() =(0,1,
=(0,1,![]() ),∴
),∴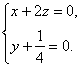
令x=2,则x=-1,y=![]() .∴n=(2,
.∴n=(2,![]() ,-1).?
,-1).?
由题意CA=CB,E为AB的中点,∴CE⊥AB.?
又三棱柱ABC—A1B
∴CE⊥平面A1EF,?
![]() =(
=(![]() ,
,![]() ,0)为平面A1EF的法向量. ?
,0)为平面A1EF的法向量. ?
∴Cos〈n,![]() 〉=
〉= .?
.?
∴〈n,![]() 〉=45°.?
〉=45°.?
∴二面角CA1FE的大小为45°. ?
(2)向量![]() 在平面CA
在平面CA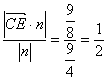 .?
.?
向量CE在平面A1CF的法向量n上的投影长即为点E到平面A1CF的距离.?
∴点E到平面A1CF的距离为![]() . ?
. ?