题目内容
平行六面体ABCD—A1B1C1D1中,AB=4,AD=3,AA1=5,∠BAD=90º ,
∠BAA1=∠DAA1=60º ,求AC1的长。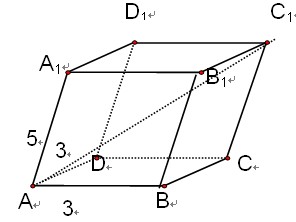

解析试题分析:连接AC,∵AB=3,AD=3,∠BAD=90°,∴AC=5,根据cos∠A1AB=cos∠A1AC•cos∠CAB,即 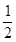 =cos∠A1AC•
=cos∠A1AC• ,∴∠A1AC=45°则∠C1CA=135°,而AC=5,AA1=5,根据余弦定理得AC1=
,∴∠A1AC=45°则∠C1CA=135°,而AC=5,AA1=5,根据余弦定理得AC1= 。
。
考点:本题考查点、线、面间的距离计算;余弦定理。
点评:本题以平行六面体为载体,考查了空间想象能力,计算推理的能力,属于中档题.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
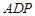 的最大面积及相应的x值.
的最大面积及相应的x值.
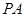 垂直于⊙
垂直于⊙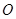 所在的平面,
所在的平面,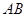 是⊙
是⊙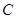 是⊙
是⊙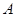 作
作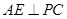 ,垂足为
,垂足为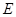 .
. 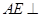 平面
平面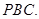

 中,
中,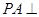 底面
底面 ,点
,点 ,
, 分别在棱
分别在棱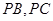 上,且
上,且
 平面
平面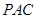 ;
; 的中点时,求
的中点时,求 与平面
与平面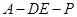 为直二面角?并说明理由.
为直二面角?并说明理由.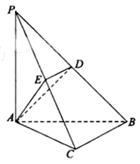
 的正方体
的正方体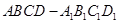 中,M,N分别是棱CD,AD的中点。(1)求证:四边形
中,M,N分别是棱CD,AD的中点。(1)求证:四边形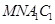 是梯形;(2)求证:
是梯形;(2)求证: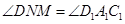

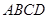 关于直线
关于直线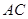 对称,
对称,
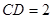 。
。 沿
沿 折起(如图二),使二面角
折起(如图二),使二面角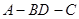 的余弦值等于
的余弦值等于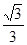 。对于图二,
。对于图二,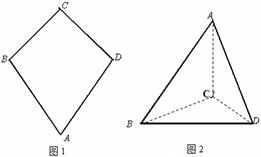
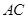 ;
;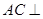 平面
平面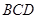 ;
; 所成角的正弦值。
所成角的正弦值。
 ,直线PB与CD所成角为
,直线PB与CD所成角为 ,
,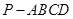 中,平面
中,平面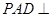 平面
平面 ,
,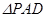 为等边三角形,底面
为等边三角形,底面 为菱形,
为菱形,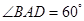 ,
,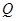 为
为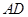 的中点,
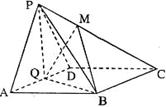
的中点,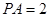 。
。
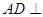 平面
平面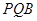 ;
;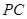 上是否存在点
上是否存在点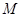 ,使
,使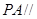 平面
平面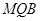 ; 若存在,求出
; 若存在,求出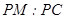 的值。
的值。