题目内容
四面体ABCD四个面的重心分别为E、F、G、H，则四面体EFGH的表面积与四面体ABCD的表面积的比值是（ ）A．
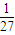
B．
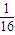
C．
D．
【答案】分析：连接AF、AG并延长与BC、CD相交于M、N，推出四面体EFGH与四面体ABCD是相似的，可求出它们的相似比，面积比是相似比的平方．
解答：
解：如图，连接AF、AG并延长与BC、CD相交于M、N，
由于F、G分别是三角形的重心，
所以M、N分别是BC、CD的中点，
且AF：AM=AG：AN=2：3，
所以FG：MN=2：3，
又MN：BD=1：2，所以FG：BD=1：3，
即两个四面体的相似比是1：3，
所以两个四面体的表面积的比是1：9；
故选C．
点评：本题考查棱锥的结构特征，考查作图能力，是中档题．
解答：
解：如图，连接AF、AG并延长与BC、CD相交于M、N，由于F、G分别是三角形的重心，
所以M、N分别是BC、CD的中点，
且AF：AM=AG：AN=2：3，
所以FG：MN=2：3，
又MN：BD=1：2，所以FG：BD=1：3，
即两个四面体的相似比是1：3，
所以两个四面体的表面积的比是1：9；
故选C．
点评：本题考查棱锥的结构特征，考查作图能力，是中档题．
练习册系列答案
高中必刷题系列答案
相关题目
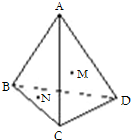在四面体ABCD中，M、N分别是面△ACD、△BCD的重心，则四面体的四个面中与MN平行的是
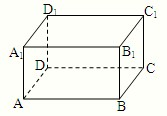如图，以长方体ABCD-A1B1C1D1的顶点A、C及另两个顶点为顶点构造四面体．