题目内容
 如图,已知AB是过抛物线y2=2px(p>0)的焦点的弦,F为抛物线的焦点,点A(x1,y1),B(x2,y2).
如图,已知AB是过抛物线y2=2px(p>0)的焦点的弦,F为抛物线的焦点,点A(x1,y1),B(x2,y2).求证:
(1)|AB|=x1+x2+p;
(2)y1 y2=-p2,x1 x2=
| p2 |
| 4 |
(3)(理科)直线的倾斜角为θ时,求弦长|AB|.
(3)(文科)当p=2,直线AB的倾斜角为
| π |
| 4 |
分析:(1)利用抛物线的定义,即可证明;
(2)设直线AB的方程为x=my+
,代入y2=2px,再利用韦达定理,即可得到结论;
(3)(理科)根据(1)的结论,表示出x1+x2即可;
(3)(文科)根据(3)(理科)的结论,即可求解.
(2)设直线AB的方程为x=my+
| p |
| 2 |
(3)(理科)根据(1)的结论,表示出x1+x2即可;
(3)(文科)根据(3)(理科)的结论,即可求解.
解答:(1)证明:∵AB是过抛物线y2=2px(p>0)的焦点的弦,
∴由抛物线定义可得|AB|=x1+
+x2+
=x1+x2+p;
(2)证明:设直线AB的方程为x=my+
,代入y2=2px,可得y2-2pmy-p2=0
∴y1y2=-p2,∴x1x2=
;
(3)(理科)解:由(2)知,y1y2=-p2,y1+y2=2pm,∴
+
=(y1+y2)2-2y1y2=4p2m2+2p2,
∴
+
=2p(x1+x2)=4p2m2+2p2,∴x1+x2=2pm2+p,
∴θ=90°时,m=0,∴|AB|=2p;θ≠90°时,m=
,|AB|=
+2p;
(4)(文科)由(3)(理科)知,|AB|=
+2p=8.
∴由抛物线定义可得|AB|=x1+
| p |
| 2 |
| p |
| 2 |
(2)证明:设直线AB的方程为x=my+
| p |
| 2 |
∴y1y2=-p2,∴x1x2=
| p2 |
| 4 |
(3)(理科)解:由(2)知,y1y2=-p2,y1+y2=2pm,∴
| y | 2 1 |
| y | 2 2 |
∴
| y | 2 1 |
| y | 2 2 |
∴θ=90°时,m=0,∴|AB|=2p;θ≠90°时,m=
| 1 |
| tanθ |
| 2p |
| tan2θ |
(4)(文科)由(3)(理科)知,|AB|=
| 2p |
| tan2θ |
点评:本题考查直线与抛物线的位置关系,考查韦达定理的运用,考查弦长的计算,属于中档题.

练习册系列答案
 优百分课时互动系列答案
优百分课时互动系列答案
相关题目
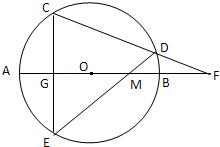 如图,已知AB是⊙O的直径,过OA的中点G作弦CE⊥AB于G,点D为优弧CBE上(除点B外)一动点,过D分别作直线CD,ED交直线AB于点F,M.
如图,已知AB是⊙O的直径,过OA的中点G作弦CE⊥AB于G,点D为优弧CBE上(除点B外)一动点,过D分别作直线CD,ED交直线AB于点F,M. 如图,已知AB是⊙O的直径,点C是⊙O上的动点(异于A、B),过动点C的直线VC垂直于⊙O所在的平面,D,E分别是VA,VC的中点.
如图,已知AB是⊙O的直径,点C是⊙O上的动点(异于A、B),过动点C的直线VC垂直于⊙O所在的平面,D,E分别是VA,VC的中点. (2011•东城区模拟)如图,已知AB是圆O的直径,AB=4,C为圆上任意一点,过C点做圆的切线分别与过A,B两点的切线交于P,Q点,则CP•CQ=
(2011•东城区模拟)如图,已知AB是圆O的直径,AB=4,C为圆上任意一点,过C点做圆的切线分别与过A,B两点的切线交于P,Q点,则CP•CQ=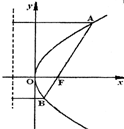 如图,已知AB是过抛物线y2=2px(p>0)的焦点的弦,F为抛物线的焦点,点A(x1,y1),B(x2,y2).
如图,已知AB是过抛物线y2=2px(p>0)的焦点的弦,F为抛物线的焦点,点A(x1,y1),B(x2,y2). ;
; 时,求弦长|AB|.
时,求弦长|AB|.