题目内容
函数y=|x|的图象与x轴、定直线x=-1及动直线x=t(t∈[-1,1])所围成图形(位于两条平行直线x=-1与x=t之间的部分)的面积为S,则S关于t的函数关系式S=f(t)= .
【答案】分析:先由题意画出图形,再根据三角形的面积公式,结合图求出对应图形的面积.
解答:解:根据题意在坐标系中画出函数的图象:
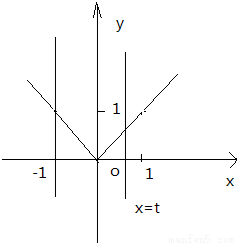
当-1≤t≤0时,s= ×1×1-
×1×1- ×t×t=
×t×t= -
-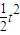 ;当0<t≤1时,s=
;当0<t≤1时,s= +
+ ×t×t=
×t×t=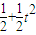 ,
,
∴s=f(t)=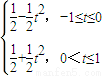 ,
,
故答案为: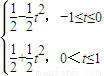 .
.
点评:本题考查了分段函数的解析式的求法,对于图形面积问题应先画出图形,再分类讨论求出对应的关系式.
解答:解:根据题意在坐标系中画出函数的图象:
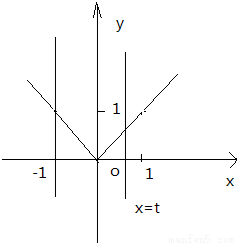
当-1≤t≤0时,s=
 ×1×1-
×1×1- ×t×t=
×t×t= -
-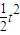 ;当0<t≤1时,s=
;当0<t≤1时,s= +
+ ×t×t=
×t×t=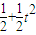 ,
,∴s=f(t)=
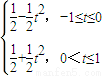 ,
,故答案为:
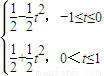 .
.点评:本题考查了分段函数的解析式的求法,对于图形面积问题应先画出图形,再分类讨论求出对应的关系式.

练习册系列答案
相关题目