题目内容
下列有五个命题:
①若sinα+cosα=1,则sinα•cosα=0.
②在同一坐标系中,函数y=sinx的图象和函数y=x的图象有三个公共点.
③函数y=tanx的图象的对称中心一定是(kπ,0),k∈Z.
④x∈R,函数y=sinx+3|sinx|的值域为[0,4].
⑤在△ABC中,若有关系式tanA=
成立,则△ABC为A=60°的三角形.
其中真命题的序号是
①若sinα+cosα=1,则sinα•cosα=0.
②在同一坐标系中,函数y=sinx的图象和函数y=x的图象有三个公共点.
③函数y=tanx的图象的对称中心一定是(kπ,0),k∈Z.
④x∈R,函数y=sinx+3|sinx|的值域为[0,4].
⑤在△ABC中,若有关系式tanA=
| cosB-cosC | sinC-sinB |
其中真命题的序号是
①⑤
①⑤
.分析:①若sinα+cosα=1,两边平方可得1+2sinαcosα=1,0.可判断①;②在同一坐标系中,函数y=sinx的图象和函数y=x的图象有一个公共点,可判断②;③函数y=tanx的图象的对称中心一定是(
kπ,0),④x∈R,函数y=sinx+3|sinx|
,结合函数的性质可得值域⑤在△ABC中,若有关系式tanA=
成立,则cos(A-B)=cos(A-C ),由原式可得sinA≠sinB,可判断⑤
| 1 |
| 2 |
|
| cosB-cosC |
| sinC-sinB |
解答:解:①若sinα+cosα=1,两边平方可得1+2sinαcosα=1,则sinα•cosα=0.故①正确
②在同一坐标系中,函数y=sinx的图象和函数y=x的图象有一个公共点.故②错误
③函数y=tanx的图象的对称中心一定是(
kπ,0),k∈Z.故③错误
④x∈R,函数y=sinx+3|sinx|=
的值域为[-2,4].故④错误
⑤在△ABC中,若有关系式tanA=
成立,则
=
∴sinAsinC-sinAsinB=cosAcosB-cosAcosC
∴cos(A-B)=cos(A-C )
但由原式可得sinA≠sinB,则A-B=C-A
∴B+C=2A,再由A+B+C=180°可得A=60°故⑤正确
故答案为:①⑤
②在同一坐标系中,函数y=sinx的图象和函数y=x的图象有一个公共点.故②错误
③函数y=tanx的图象的对称中心一定是(
| 1 |
| 2 |
④x∈R,函数y=sinx+3|sinx|=
|
⑤在△ABC中,若有关系式tanA=
| cosB-cosC |
| sinC-sinB |
| sinA |
| cosA |
| cosB-cosC |
| sinC-sinB |
∴sinAsinC-sinAsinB=cosAcosB-cosAcosC
∴cos(A-B)=cos(A-C )
但由原式可得sinA≠sinB,则A-B=C-A
∴B+C=2A,再由A+B+C=180°可得A=60°故⑤正确
故答案为:①⑤
点评:本题主要考查了同角平方关系、正弦函数的图象及函数的性质的应用,正切函数的性质的考查,两角差的余弦公式顶的应用,属于知识的综合应用.

练习册系列答案
相关题目
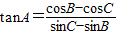 成立,则△ABC为A=60°的三角形.
成立,则△ABC为A=60°的三角形.