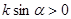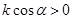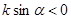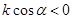题目内容
已知平面内两定点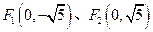 ,动点
,动点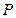 满足条件:
满足条件: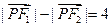 ,设点
,设点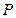 的轨迹是曲线
的轨迹是曲线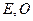 为坐标原点。
为坐标原点。
(I)求曲线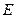 的方程;
的方程;
(II)若直线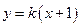 与曲线
与曲线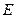 相交于两不同点
相交于两不同点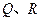 ,求
,求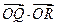 的取值范围;
的取值范围;
(III)(文科做)设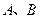 两点分别在直线
两点分别在直线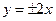 上,若
上,若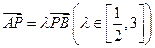 ,记
,记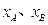 分别为
分别为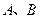 两点的横坐标,求
两点的横坐标,求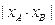 的最小值。
的最小值。
(理科做)设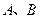 两点分别在直线
两点分别在直线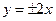 上,若
上,若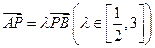 ,求
,求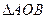 面积的最大值。
面积的最大值。
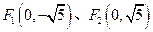 ,动点
,动点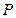 满足条件:
满足条件: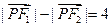 ,设点
,设点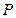 的轨迹是曲线
的轨迹是曲线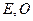 为坐标原点。
为坐标原点。(I)求曲线
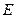 的方程;
的方程;(II)若直线
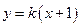 与曲线
与曲线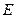 相交于两不同点
相交于两不同点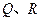 ,求
,求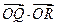 的取值范围;
的取值范围;(III)(文科做)设
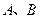 两点分别在直线
两点分别在直线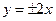 上,若
上,若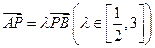 ,记
,记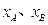 分别为
分别为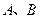 两点的横坐标,求
两点的横坐标,求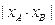 的最小值。
的最小值。(理科做)设
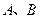 两点分别在直线
两点分别在直线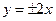 上,若
上,若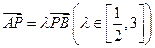 ,求
,求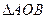 面积的最大值。
面积的最大值。见解析




练习册系列答案
相关题目
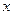 轴上,它的一个顶点为
轴上,它的一个顶点为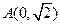 ,且离心率等于
,且离心率等于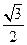 ,过点
,过点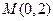 的直线
的直线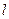 与椭圆相交于不同两点
与椭圆相交于不同两点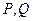 ,点
,点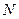 在线段
在线段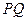 上。
上。
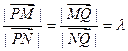 ,若直线
,若直线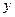 轴不重合,
轴不重合,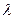 的取值范围。
的取值范围。 :
: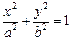 (
(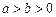 ),其左、右焦点分别为
),其左、右焦点分别为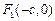 、
、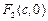 ,且
,且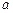 、
、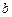 、
、 成等比数列.
成等比数列.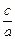 的值.
的值.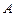 、
、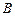 ,求证:
,求证: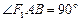 .
.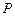 为椭圆
为椭圆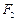 、
、 ,使
,使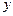 轴的交点
轴的交点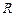 满足
满足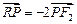 ?若存在,求直线
?若存在,求直线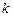 ;若不存在,请说明理由.
;若不存在,请说明理由.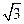 B.
B.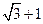
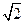 D.
D.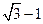

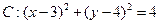 和直线
和直线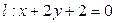 ,直线
,直线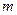 ,
,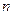 都经过圆C外
都经过圆C外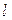 交于N点,且线段PQ的中点为M,
交于N点,且线段PQ的中点为M,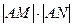 为定值.
为定值.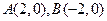 ,
,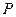 是平面内一动点,直线
是平面内一动点,直线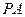 、
、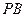 斜率之积为
斜率之积为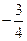 。
。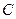 的方程;
的方程;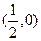 作直线
作直线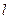 与轨迹
与轨迹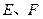 两点,线段
两点,线段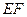 的中点为
的中点为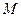 ,求直线
,求直线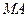 的斜率
的斜率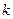 的取值范围。
的取值范围。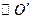 过定点
过定点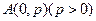 ,圆心
,圆心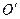 在抛物线
在抛物线 :
: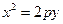 上运动,
上运动,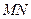 为圆
为圆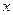 轴上所截得的弦.
轴上所截得的弦.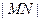 是否有变化?并证明你的结论;
是否有变化?并证明你的结论;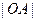 是
是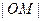 与
与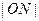 的等差中项时,
的等差中项时,
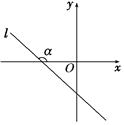
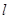 经过二、三、四象限,
经过二、三、四象限,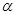 ,斜率为k,则 ( ).
,斜率为k,则 ( ).