题目内容
已知向量
(1)证明:
(2)若向量满足 ,且
,且 ,求
,求 .
.
(1)见解析;(2) 或
或 .
.
解析试题分析:(1)根据题中条件先求出向量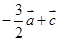 与
与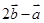 的坐标,再根据向量共线的充要条件进行判定;(2)设出向量
的坐标,再根据向量共线的充要条件进行判定;(2)设出向量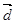 的坐标,算出向量
的坐标,算出向量 、
、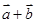 、
、 坐标,根据向量垂直的充要条件和模公式,列出关于向量
坐标,根据向量垂直的充要条件和模公式,列出关于向量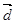 坐标的方程组,通过解方程组解出向量
坐标的方程组,通过解方程组解出向量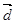 .
.
试题解析:(1)因为向量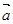
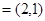 ,
,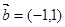 ,
,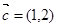
所以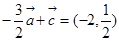 ,
,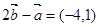 , 3分
, 3分
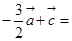
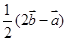 5分
5分
所以 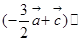
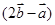 6分
6分
(2)设向量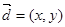 ,
,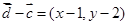 ,
,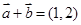
因为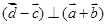 , 所以
, 所以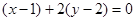
即 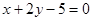 (1) 8分
(1) 8分
又 ,所以
,所以
即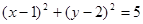 (2) 10分
(2) 10分
由(1)(2)得: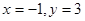 或
或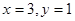
所以 或
或 12分
12分
考点:向量的坐标运算;向量平行的充要条件;向量垂直的充要条件;向量的模公式;方程思想

练习册系列答案
相关题目
 是奇函数,则
是奇函数,则 ;
; :事件
:事件 是对立事件;
是对立事件; :事件
:事件 (
( 为自然对数的底);
为自然对数的底); ,
, ,则
,则 在
在 上的投影为
上的投影为 ;
; ,则
,则 .
.
 ,试求
,试求 的值;
的值; ,试求
,试求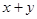 的值;
的值;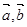 满足
满足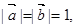 ,且
,且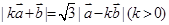 ,令
,令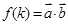 .
.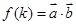 (用
(用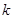 表示);
表示);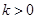 时,
时,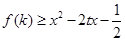 对任意的
对任意的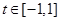 恒成立,求实数
恒成立,求实数 的取值范围。
的取值范围。 的三个内角
的三个内角 所对的边分别为
所对的边分别为 ,向量
,向量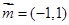 ,
,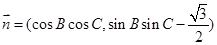 ,且
,且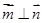 .
.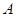 的大小;
的大小;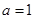 ;②
;②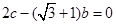 ;③
;③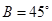 ,试从中再选择两个条件以确定
,试从中再选择两个条件以确定 ,θ为a与b的夹角.
,θ为a与b的夹角. sin2(θ-x),求f(x)的单调递增区间.
sin2(θ-x),求f(x)的单调递增区间. 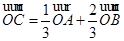
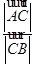 的值;
的值; ,
, 的最小值为
的最小值为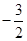 ,求实数m的值.
,求实数m的值.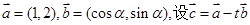 (
( 为实数).
为实数).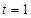 时,若
时,若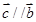 ,求
,求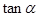 ;
;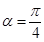 ,求
,求 的最小值,并求出此时向量
的最小值,并求出此时向量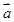 在
在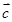 方向上的投影.
方向上的投影. ·
· -
- 2=0,则△ABC的面积为________.
2=0,则△ABC的面积为________.