题目内容
在平面直角坐标系中,O为坐标原点,A、B、C三点满足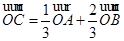
(1)求证:A、B、C三点共线;
(2)求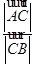 的值;
的值;
(3)已知 ,
, 的最小值为
的最小值为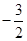 ,求实数m的值.
,求实数m的值.
(1)详见解析;(2)2;(3) .
.
解析试题分析:(1)要证 三点共线,即证
三点共线,即证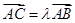 ,根据
,根据 ,
,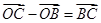 化简;
化简;
(2)根据第一问,三点共线,可化简为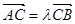 ;
;
(3)根据向量的数量积与模的公式可将函数化简, ,
,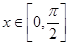 ,然后分
,然后分
 ,
, 三种情况进行讨论,求最小值.
三种情况进行讨论,求最小值.
解:(1)由已知 ,即
,即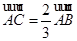 ,
,
∴ ∥
∥ . 又∵
. 又∵ 、
、 有公共点
有公共点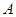 ,∴A、B、C三点共线. 4分
,∴A、B、C三点共线. 4分
(2)∵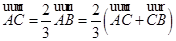 ,∴
,∴ 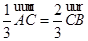
∴
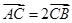 ,∴
,∴ 。 7分
。 7分
(3)∵C为 的定比分点,λ=2,∴
的定比分点,λ=2,∴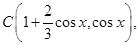
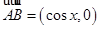

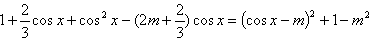
∵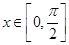 ,∴
,∴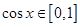
当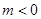 时,当
时,当 时,f(x)取最小值
时,f(x)取最小值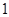 与已知相矛盾;
与已知相矛盾;
当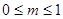 时, 当
时, 当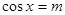 时, f(x)取最小值
时, f(x)取最小值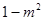 ,得
,得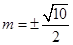 (舍)
(舍)
当 时,当
时,当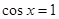 时,f(x)取得最小值
时,f(x)取得最小值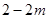 ,得
,得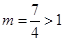 ,
,
综上所述, 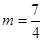 为所求. 13分
为所求. 13分
考点:1.向量共线的充要条件;2.向量的加减法;3.向量数量积的化简;4.二次函数求最值.

练习册系列答案
相关题目
已知数列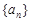 的通项公式
的通项公式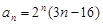 ,则数列
,则数列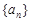 的前
的前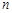 项和
项和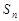 取得最小值时
取得最小值时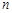 的值为( )
的值为( )
A.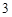 | B.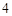 | C.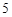 | D. |
 是平面上一点,
是平面上一点, 是平面上不共线三点,动点
是平面上不共线三点,动点 满足:
满足: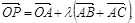
 ,已知
,已知 时,
时, .则
.则 的最小值____________.
的最小值____________.

 ,且
,且 ,求
,求 .
. 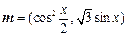 ,
,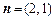 ,函数
,函数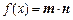 .
.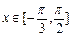 时,求函数
时,求函数 的取值范围;
的取值范围;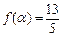 ,且
,且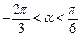 时,求
时,求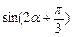 的值.
的值.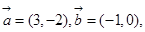
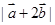 ;
;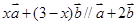 时,求
时,求 的值.
的值. -t
-t )·
)·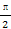 ).
).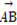 ⊥a,且|
⊥a,且|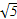 |
| |(O为坐标原点),求向量
|(O为坐标原点),求向量 .
.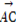 与向量a共线,当k>4,且tsinθ取最大值4时,求
与向量a共线,当k>4,且tsinθ取最大值4时,求 .
. AC,在AB上取点M,使得AM=
AC,在AB上取点M,使得AM= BN,在CM的延长线上取一点Q,使MQ=λCM时,
BN,在CM的延长线上取一点Q,使MQ=λCM时, =
=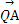 ,试确定λ的值.
,试确定λ的值.