题目内容
椭圆的两焦点坐标分别为F1(-
,0)和F2(
,0),且椭圆过点(1,-
).
(1)求椭圆方程;
(2)过点(-
,0)作不与y轴垂直的直线l交该椭圆于M、N两点,A为椭圆的左顶点,试判断∠MAN的大小是否为定值,并说明理由.
| 3 |
| 3 |
| ||
| 2 |
(1)求椭圆方程;
(2)过点(-
| 6 |
| 5 |
(1)设椭圆的方程为
+
=1
∵焦点坐标为F1(-
,0)与F2(
,0)
∴a2=3+b2①
∵椭圆过点(1,-
)
∴
+
=1②
解得a2=4,b2=3
所以椭圆方程为
+y2=1
(2)设直线MN的方程为:x=ky-
,
联立直线MN和曲线C的方程可得:
得:(k2+4)y2-
ky-
=0,
设M(x1,y1),N(x2,y2),A(-2,0),
则y1+y2=
,y1•y2=-
则
•
=(x1+2,y1)•(x2+2,y2)=(k2+1)y1y2+
k(y1+y2)+
=0
即可得,∠MAN=
.
| x2 |
| a2 |
| y2 |
| b2 |
∵焦点坐标为F1(-
| 3 |
| 3 |
∴a2=3+b2①
∵椭圆过点(1,-
| ||
| 2 |
∴
| 1 |
| a2 |
| 3 |
| 4b2 |
解得a2=4,b2=3
所以椭圆方程为
| x2 |
| 4 |
(2)设直线MN的方程为:x=ky-
| 6 |
| 5 |
联立直线MN和曲线C的方程可得:
|
得:(k2+4)y2-
| 12 |
| 5 |
| 64 |
| 25 |
设M(x1,y1),N(x2,y2),A(-2,0),
则y1+y2=
| 12k |
| 5(k2+4) |
| 64 |
| 25(k2+4) |
则
| AM |
| AN |
| 4 |
| 5 |
| 16 |
| 25 |
即可得,∠MAN=
| π |
| 2 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
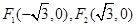 ,且椭圆过点
,且椭圆过点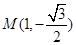 .
.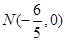 作不与
作不与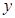 轴垂直的直线
轴垂直的直线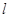 交该椭圆于
交该椭圆于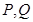 两点,
两点,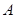 为椭圆的左顶点,试判断
为椭圆的左顶点,试判断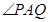 的大小是否为定值,并说明理由.
的大小是否为定值,并说明理由.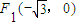 和
和 ,且椭圆过点
,且椭圆过点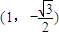 .
. 作不与y轴垂直的直线l交该椭圆于M、N两点,A为椭圆的左顶点,试判断∠MAN的大小是否为定值,并说明理由.
作不与y轴垂直的直线l交该椭圆于M、N两点,A为椭圆的左顶点,试判断∠MAN的大小是否为定值,并说明理由.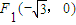 和
和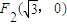 ,且椭圆过点
,且椭圆过点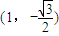 .
.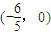 作不与y轴垂直的直线l交该椭圆于M、N两点,A为椭圆的左顶点,试判断∠MAN的大小是否为定值,并说明理由.
作不与y轴垂直的直线l交该椭圆于M、N两点,A为椭圆的左顶点,试判断∠MAN的大小是否为定值,并说明理由.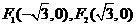 ,且椭圆过点
,且椭圆过点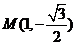 .
.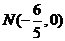 作不与
作不与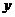 轴垂直的直线
轴垂直的直线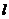 交该椭圆于
交该椭圆于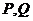 两点,
两点,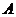 为椭圆的左顶点,试判断
为椭圆的左顶点,试判断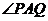 的大小是否为定值,并说明理由.
的大小是否为定值,并说明理由.