题目内容
【题目】设函数f(x)= ![]() (x>0),数列{an}满足
(x>0),数列{an}满足 ![]() (n∈N* , 且n≥2).
(n∈N* , 且n≥2).
(1)求数列{an}的通项公式;
(2)设Tn=a1a2﹣a2a3+a3a4﹣a4a5+…+(﹣1)n﹣1anan+1 , 若Tn≥tn2对n∈N*恒成立,求实数t的取值范围;
(3)是否存在以a1为首项,公比为q(0<q<5,q∈N*)的数列{a ![]() },k∈N* , 使得数列{a
},k∈N* , 使得数列{a ![]() }中每一项都是数列{an}中不同的项,若存在,求出所有满足条件的数列{nk}的通项公式;若不存在,说明理由.
}中每一项都是数列{an}中不同的项,若存在,求出所有满足条件的数列{nk}的通项公式;若不存在,说明理由.
【答案】
(1)解:因为 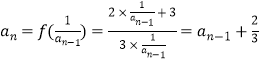 ,(n∈N*,且n≥2),
,(n∈N*,且n≥2),
所以an﹣an﹣1= ![]() .
.
因为a1=1,
所以数列{an}是以1为首项,公差为 ![]() 的等差数列.
的等差数列.
所以an= ![]()
(2)解:①当n=2m,m∈N*时,Tn=T2m=a1a2﹣a2a3+a3a4﹣a4a5++(﹣1)2m﹣1a2ma2m+1=a2(a1﹣a3)+a4(a3﹣a5)++a2m(a2m﹣1﹣a2m+1)=﹣ ![]() =﹣
=﹣ ![]() =﹣
=﹣ ![]() .
.
②当n=2m﹣1,m∈N*时,Tn=T2m﹣1=T2m﹣(﹣1)2m﹣1a2ma2m+1=﹣ ![]() =
= ![]() .
.
所以Tn= 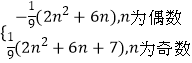
要使Tn≥tn2对n∈N*恒成立,
只要使﹣ ![]() ,(n为偶数)恒成立.
,(n为偶数)恒成立.
只要使﹣ ![]() ,对n为偶数恒成立,
,对n为偶数恒成立,
故实数t的取值范围为 ![]()
(3)解:由an= ![]() ,知数列{an}中每一项都不可能是偶数.
,知数列{an}中每一项都不可能是偶数.
①如存在以a1为首项,公比q为2或4的数列{ank},k∈N*,
此时{ank}中每一项除第一项外都是偶数,故不存在以a1为首项,公比为偶数的数列{ank}.
②当q=1时,显然不存在这样的数列{ank}.
当q=3时,若存在以a1为首项,公比为3的数列{ank},k∈N*.
则 ![]() =1,n1=1,
=1,n1=1, ![]() =
= ![]() ,nk=
,nk= ![]() .
.
所以满足条件的数列{nk}的通项公式为nk= ![]()
【解析】(1)由 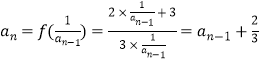 ,(n∈N* , 且n≥2),知
,(n∈N* , 且n≥2),知 ![]() .再由a1=1,能求出数列{an}的通项公式;(2)当n=2m,m∈N*时,Tn=T2m=a1a2﹣a2a3+a3a4﹣a4a5++(﹣1)2m﹣1a2ma2m+1=a2(a1﹣a3)+a4(a3﹣a5)++a2m(a2m﹣1﹣a2m+1)=
.再由a1=1,能求出数列{an}的通项公式;(2)当n=2m,m∈N*时,Tn=T2m=a1a2﹣a2a3+a3a4﹣a4a5++(﹣1)2m﹣1a2ma2m+1=a2(a1﹣a3)+a4(a3﹣a5)++a2m(a2m﹣1﹣a2m+1)= ![]() =
= ![]() =
= ![]() .当n=2m﹣1,m∈N*时,Tn=T2m﹣1=T2m﹣(﹣1)2m﹣1a2ma2m+1=
.当n=2m﹣1,m∈N*时,Tn=T2m﹣1=T2m﹣(﹣1)2m﹣1a2ma2m+1= ![]() =
= ![]() .由此入手能求出实数t的取值范围.(3)由
.由此入手能求出实数t的取值范围.(3)由 ![]() ,知数列{an}中每一项都不可能是偶数.如存在以a1为首项,公比q为2或4的数列{ank},k∈N* , 此时{ank}中每一项除第一项外都是偶数,故不存在以a1为首项,公比为偶数的数列{ank}.当q=1时,显然不存在这样的数列{ank}.当q=3时,
,知数列{an}中每一项都不可能是偶数.如存在以a1为首项,公比q为2或4的数列{ank},k∈N* , 此时{ank}中每一项除第一项外都是偶数,故不存在以a1为首项,公比为偶数的数列{ank}.当q=1时,显然不存在这样的数列{ank}.当q=3时, ![]() ,n1=1,
,n1=1, ![]() ,
, ![]() .所以满足条件的数列{nk}的通项公式为
.所以满足条件的数列{nk}的通项公式为 ![]() .
.

【题目】某种多面体玩具共有12个面,在其十二个面上分别标有数字1,2,3,…,12.若该玩具质地均匀,则抛掷该玩具后,任何一个数字所在的面朝上的概率均相等.
为检验某批玩具是否合格,制定检验标准为:多次抛掷该玩具,并记录朝上的面上标记的数字,若各数字出现的频率的极差不超过0.05.则认为该玩具合格.

(1)对某批玩具中随机抽取20件进行检验,将每个玩具各面数字出现频率的极差绘制成茎叶图(如图所示),试估计这批玩具的合格率;
(2)现有该种类玩具一个,将其抛掷100次,并记录朝上的一面标记的数字,得到如下数据:
朝上面的数字 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
次数 | 9 | 7 | 8 | 6 | 10 | 9 | 9 | 8 | 10 | 9 | 7 | 8 |
1)试判定该玩具是否合格;
2)将该玩具抛掷一次,记事件![]() :向上的面标记数字是完全平方数(能写成整数的平方形式的数,如
:向上的面标记数字是完全平方数(能写成整数的平方形式的数,如![]() ,9为完全平方数);事件
,9为完全平方数);事件![]() :向上的面标记的数字不超过4.试根据上表中的数据,完成以下列联表(其中
:向上的面标记的数字不超过4.试根据上表中的数据,完成以下列联表(其中![]() 表示
表示![]() 的对立事件),并回答在犯错误的概率不超过0.01的前提下,能否认为事件
的对立事件),并回答在犯错误的概率不超过0.01的前提下,能否认为事件![]() 与事件
与事件![]() 有关.
有关.
|
| 合计 | |
| |||
| |||
合计 | 100 |
(参考公式及数据: 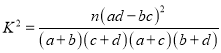 ,
, ![]() )
)
