题目内容
已知数列![]() 满足:
满足:![]() ,
,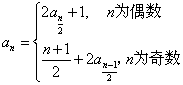
![]()
(I)求![]() 的值;
的值;
(II)设![]() ,试求数列
,试求数列![]() 的通项公式;
的通项公式;
(III) 对任意的正整数![]() ,试讨论
,试讨论![]() 与
与![]() 的大小关系.
的大小关系.
解:(Ⅰ)∵ ![]() ,
,![]() ,
,![]() ,
,![]() ,
,
∴ ![]() ;
;![]() ;
;![]() . ………………3分
. ………………3分
(Ⅱ)由题设,对于任意的正整数![]() ,都有:
,都有:![]() ,
,
∴ ![]() .∴ 数列
.∴ 数列![]() 是以
是以![]() 为首项,
为首项,![]() 为公差的等差数列.
为公差的等差数列.
∴ ![]() . …………………………………………………………6分
. …………………………………………………………6分
(Ⅲ)对于任意的正整数![]() ,
,
当![]() 或
或![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() . ……………………………………8分
. ……………………………………8分
证明如下:
首先,由![]() 可知
可知![]() 时,
时,![]() ;
;
其次,对于任意的正整数![]() ,
,
![]() 时,
时,![]() ;
;
…………………9分
![]() 时,
时,![]()
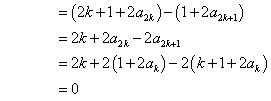
所以,![]() . …………………10分
. …………………10分
![]() 时,
时,![]()
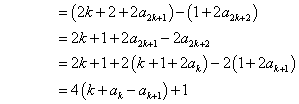
事实上,我们可以证明:对于任意正整数![]() ,
,![]() (*)(证明见后),所以,此时,
(*)(证明见后),所以,此时,![]() .
.
综上可知:结论得证.
对于任意正整数![]() ,
,![]() (*)的证明如下:
(*)的证明如下:
1)当![]() (
(![]() )时,
)时,
![]() ,
,
满足(*)式。
2)当![]() 时,
时,![]() ,满足(*)式。
,满足(*)式。
3)当![]() 时,
时,
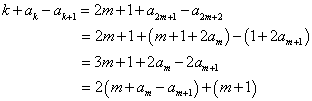
于是,只须证明![]() ,如此递推,可归结为1)或2)的情形,于是(*)得证. …………………12分
,如此递推,可归结为1)或2)的情形,于是(*)得证. …………………12分

练习册系列答案
相关题目
 满足
满足 ,则此数列的通项
,则此数列的通项 等于
等于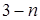 B.
B. C.
C.  D.
D. 
 满足:
满足: .
. ;
; ,求数列
,求数列 的通项公式;
的通项公式; ,不等式
,不等式 恒成立时,求实数
恒成立时,求实数 的取值范围.
的取值范围.