题目内容
(2012•芜湖三模)已知数列满足a1+2a2+…+2n-1an=
(n∈N+).
(Ⅰ)求数列{an}的通项;
(Ⅱ)若bn=
,求数列{bn}的前n和Sn;
(Ⅲ)求证Sn≥n2+2n-1.
| n |
| 2 |
(Ⅰ)求数列{an}的通项;
(Ⅱ)若bn=
| n |
| an |
(Ⅲ)求证Sn≥n2+2n-1.
分析:( I)由n=1,可求a1=
,由已知可得n≥2时,a1+2a2+…+2n-2an-1=
,两式相减可求an
(II)由(I)可得bn=
=n•2n,利用错位相减可求和
(III)由(II)可知,Sn-2=(n-1)•2n+1=(n-1)•(1+1)n,只要证明Sn-2>0即可
| 1 |
| 2 |
| n-1 |
| 2 |
(II)由(I)可得bn=
| n |
| an |
(III)由(II)可知,Sn-2=(n-1)•2n+1=(n-1)•(1+1)n,只要证明Sn-2>0即可
解答:解:( I)n=1时,a1=
∵a1+2a2+…+2n-1an=
∴n≥2时,a1+2a2+…+2n-2an-1=
两式相减可得,2n-1an=
∴an=
(II)解:∵bn=
=n•2n
∴Sn=1•2+2•22+3•23+…+n•2n
2Sn=1•22+2•23+…+n•2n+1
两式相减可得,-Sn=2+22+23+…+2n-n•2n+1=
-n•2n+1
∴Sn=(n-1)•2n+1+2
(III)证明:由(II)可知,Sn-2=(n-1)•2n+1=(n-1)•(1+1)n
=(n-1)(
+
+…+
)≥(n-1)(
+
+
)=(n-1)(n+3)=n2+2n-3
∴Sn-2≥n2-2n-3
∴Sn≥n2+2n-1
| 1 |
| 2 |
∵a1+2a2+…+2n-1an=
| n |
| 2 |
∴n≥2时,a1+2a2+…+2n-2an-1=
| n-1 |
| 2 |
两式相减可得,2n-1an=
| 1 |
| 2 |
∴an=
| 1 |
| 2n |
(II)解:∵bn=
| n |
| an |
∴Sn=1•2+2•22+3•23+…+n•2n
2Sn=1•22+2•23+…+n•2n+1
两式相减可得,-Sn=2+22+23+…+2n-n•2n+1=
| 2(1-2n) |
| 1-2 |
∴Sn=(n-1)•2n+1+2
(III)证明:由(II)可知,Sn-2=(n-1)•2n+1=(n-1)•(1+1)n
=(n-1)(
| C | 0 n+1 |
| C | 1 n+1 |
| C | n+1 n+1 |
| C | 0 n+1 |
| C | 1 n+1 |
| C | n+1 n+1 |
∴Sn-2≥n2-2n-3
∴Sn≥n2+2n-1
点评:本题主要考查了利用递推公式求解数列的通项公式,数列的错位相减求解数列的和及利用组合数的性质证明不等式,注意放缩法在证明中的应用.

练习册系列答案
 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案
相关题目
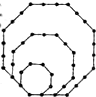 (2012•芜湖三模)如图,将边长为1,2,3的正八边形叠放在一起,同一边上相邻珠子的距离为1,若以此方式再放置边长为4,5,6,…,10的正八边形,则这10个正八边形镶嵌的珠子总数是
(2012•芜湖三模)如图,将边长为1,2,3的正八边形叠放在一起,同一边上相邻珠子的距离为1,若以此方式再放置边长为4,5,6,…,10的正八边形,则这10个正八边形镶嵌的珠子总数是