题目内容
8．已知f（2）=-$\frac{4}{3}$，f′（2）=-1，则$\underset{lim}{x→2}$$\frac{3f（x）+2x}{x-2}$的值是（ ）| A． | 1 | B． | 2 | C． | -1 | D． | -2 |
分析 根据洛必达法则求出极限值即可．
解答 解：x→2时：x-2→0，
3f（2）+2×2=0，
根据洛必达法则：
则$\underset{lim}{x→2}$$\frac{3f（x）+2x}{x-2}$=$\underset{lim}{x→2}$$\frac{3f′（x）+2}{1}$=-1，
故选：C．
点评 本题考查了导数的应用，考查洛必达法则，是一道基础题．
练习册系列答案
特高级教师点拨系列答案
相关题目
13．已知O是三角形ABC内部一点，满足$\overrightarrow{OA}$+2$\overrightarrow{OB}$=4$\overrightarrow{CO}$，则$\frac{{S}_{△AOB}}{{S}_{△AOC}}$=（ ）
| A． | $\frac{3}{2}$ | B． | 5 | C． | 2 | D． | $\frac{5}{3}$ |
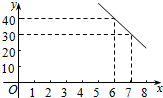某公司试销一种成本单价为50元/件的新产品，规定试销时销售单价不低于成本单价，又不高于80元/件．经试销调查，发现销售量y（件）与销售单价x（元/件）可近似看作一次函数y=kx+b的关系（如图所示）．