题目内容
14．求函数y=$\frac{{x}^{2}}{x-3}$在区间[1，2]上的最大值和最小值．分析 求函数的导数，利用函数的单调性进行求解即可．
解答 解：函数的导数为f′（x）=$\frac{2x（x-3）-{x}^{2}}{（x-3）^{2}}$=$\frac{{x}^{2}-6x}{（x-3）^{2}}$，
则当1≤x≤2时，f′（x）＜0，此时函数为减函数，
∴f（x）max=f（1）=$\frac{1}{1-3}=-\frac{1}{2}$，f（x）min=f（2）=$\frac{4}{2-3}=-4$．
点评 本题主要考查函数最值的求解，求函数的导数，利用导数研究函数的单调性是解决本题的关键．
练习册系列答案
能考试期末冲刺卷系列答案
相关题目
2．定义在R上的偶函数f（x）满足f（x+2）=f（x），且在区间[-3，-2]上是减函数，若A，B是锐角三角形的两个内角，且A＞B，则（ ）
| A． | f（sinA）＞f（cosB） | B． | f（sinA）＜f（cosB） | C． | f（sinA）＞f（sinB） | D． | f（cosA）＞f（cosB） |
3．
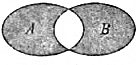如图所示的韦恩图中，A，B中两非空集合，定义集合A?B为阴影部分表示的集合，若x，y∈R，A={x|y=ln（2x-x2）}，B={y|y=ex，x＞0}，则A?B为（ ）
如图所示的韦恩图中，A，B中两非空集合，定义集合A?B为阴影部分表示的集合，若x，y∈R，A={x|y=ln（2x-x2）}，B={y|y=ex，x＞0}，则A?B为（ ）| A． | {x|0＜x＜2} | B． | {x|x≤1或x≥2} | C． | {x|0≤x≤1或x≥2} | D． | {x|0＜x≤1或x≥2} |
18．已知集合A={x|0＜x＜1|，B={x|-1≤log2x≤1}，则A∩B=（ ）
| A． | （0，2] | B． | [$\frac{1}{2}$，1） | C． | （1，2] | D． | [$\frac{1}{2}$，2] |