题目内容
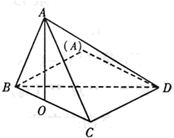 如图,矩形ABCD中,AB=3,BC=4,沿对角线BD将△ABD折起,使A点在平面BCD内的射影落在BC边上,若二面角C-AB-D的平面角大小为θ,则sinθ的值等于( )
如图,矩形ABCD中,AB=3,BC=4,沿对角线BD将△ABD折起,使A点在平面BCD内的射影落在BC边上,若二面角C-AB-D的平面角大小为θ,则sinθ的值等于( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
分析:根据已知中矩形ABCD中,AB=3,BC=4,沿对角线BD将△ABD折起,使A点在平面BCD内的射影落在BC边上,若二面角C-AB-D的平面角大小为θ,我们可以得到∠CAD是二面角C-AB-D的平面角,解三角形CAD即可得到答案.
解答:解:由AO⊥平面BCD,CD在平面BCD内,
知 AO⊥CD
又CD⊥BC,且AO交BC于O,故CD⊥平面ABC
又 AB在平面ABC内,故CD⊥AB,
又DA⊥AB,且CD交DA于D,故AB⊥平面ACD,
又 AC在平面ACD内,故AB⊥AC,
又AB⊥AD
故∠CAD是二面角C-AB-D的平面角
在△CAD中,由CD⊥平面ABC,AC在平面ABC内,可知CD⊥AC
又 CD=3,AD=4,
故sin∠CAD=
=
故选A.
知 AO⊥CD
又CD⊥BC,且AO交BC于O,故CD⊥平面ABC
又 AB在平面ABC内,故CD⊥AB,
又DA⊥AB,且CD交DA于D,故AB⊥平面ACD,
又 AC在平面ACD内,故AB⊥AC,
又AB⊥AD
故∠CAD是二面角C-AB-D的平面角
在△CAD中,由CD⊥平面ABC,AC在平面ABC内,可知CD⊥AC
又 CD=3,AD=4,
故sin∠CAD=
| CD |
| AD |
| 3 |
| 4 |
故选A.
点评:本题考查的知识点是二面角的平面角及求法,其中求出二面角的平面角是解答本题的关键.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
 如图,矩形ABCD中,AB=
如图,矩形ABCD中,AB=
 A 若方程ax-x-a=0有两个实数解,则a的取值范围是
A 若方程ax-x-a=0有两个实数解,则a的取值范围是 如图,矩形ABCD中,
如图,矩形ABCD中, (理)如图,矩形ABCD中,AB=1,BC=a,PA⊥平面ABCD
(理)如图,矩形ABCD中,AB=1,BC=a,PA⊥平面ABCD