题目内容
(本题满分15分) 已知抛物线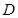 的顶点是椭圆
的顶点是椭圆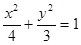 的中心,焦点与该椭圆的右焦点重合.
的中心,焦点与该椭圆的右焦点重合.
(1)求抛物线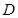 的方程;
的方程;
(2)已知动直线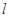 过点
过点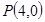 ,交抛物线
,交抛物线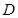 于
于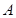 、
、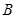 两点.
两点.
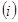 若直线
若直线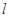 的斜率为1,求
的斜率为1,求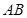 的长;
的长;
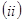 是否存在垂直于
是否存在垂直于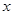 轴的直线
轴的直线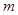 被以
被以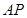 为直径的圆
为直径的圆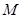 所截得的弦长恒为定值?如果存在,求出
所截得的弦长恒为定值?如果存在,求出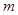 的方程;如果不存在,说明理由.
的方程;如果不存在,说明理由.
【答案】
解:(1)由题意,可设抛物线方程为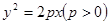 . …………1分
. …………1分
由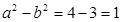 ,得
,得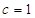 .
…………2分
.
…………2分
 抛物线的焦点为
抛物线的焦点为 ,
, .
…………3分
.
…………3分
 抛物线D的方程为
抛物线D的方程为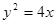 .
…………4分
.
…………4分
(2)设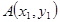 ,
,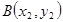 .
…………5分
.
…………5分
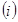 直线
直线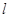 的方程为:
的方程为: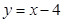 ,
…………6分
,
…………6分
联立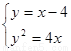 ,整理得:
,整理得: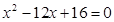 …………7分
…………7分
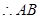 =
=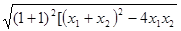
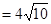 .…………9分
.…………9分
(ⅱ) 设存在直线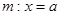 满足题意,则圆心
满足题意,则圆心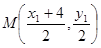 ,过
,过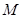 作直线
作直线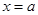 的垂线,垂足为
的垂线,垂足为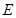 ,设直线
,设直线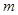 与圆
与圆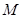 的一个交点为
的一个交点为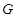 .可得:
…………10分
.可得:
…………10分
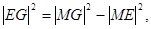 …………11分
…………11分
即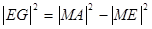 =
=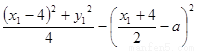
=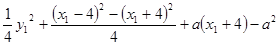
=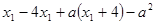 =
=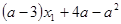 …………13分
…………13分
当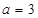 时,
时, 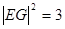 ,此时直线
,此时直线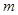 被以
被以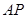 为直径的圆
为直径的圆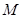 所截得的弦长恒为定值
所截得的弦长恒为定值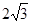 .
.
…………14分
因此存在直线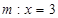 满足题意
…………15分
满足题意
…………15分
【解析】略

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
 .
. 在
在 上单调递增,在
上单调递增,在 上单调递减,求实数
上单调递减,求实数 的最大值;
的最大值; 对任意的
对任意的 ,
, 都成立,求实数
都成立,求实数 的取值范围.
的取值范围. 为自然对数的底数.
为自然对数的底数. 与曲线
与曲线 相切
相切 在
在 上恰有两个不等的实数根
上恰有两个不等的实数根 ,求
,求 的大小
的大小 :
: (
( ),焦点为
),焦点为 ,直线
,直线 交抛物线
交抛物线 、
、 两点,
两点, 是线段
是线段 的中点,
的中点, 轴的垂线交抛物线
轴的垂线交抛物线 ,
, 到焦点
到焦点 ,求此时
,求此时 的值;
的值; 是以
是以

 的单调区间;
的单调区间; ,若
,若 在
在 上不单调且仅在
上不单调且仅在 处取得最大值,求
处取得最大值,求 的取值范围.
的取值范围.