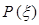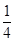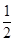题目内容
(12分)某种有奖销售的饮料,瓶盖内印有“奖励一瓶”或“谢谢购买”字样,购买一瓶若其瓶盖内印有“奖励一瓶”字样即为中奖,中奖概率为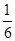 。甲、乙、丙三位同学每人购买了一瓶该饮料。
。甲、乙、丙三位同学每人购买了一瓶该饮料。
(1)求甲中奖且乙、丙没有中奖的概率;
(2)求中奖人数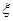 的分布列及数学期望E
的分布列及数学期望E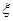 。
。
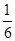 。甲、乙、丙三位同学每人购买了一瓶该饮料。
。甲、乙、丙三位同学每人购买了一瓶该饮料。(1)求甲中奖且乙、丙没有中奖的概率;
(2)求中奖人数
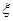 的分布列及数学期望E
的分布列及数学期望E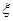 。
。;(1)P=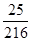 ;
;
(2)
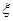 服从二项分布,E
服从二项分布,E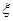 =3×
=3×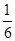 =
=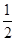 。
。
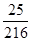 ;
;(2)
 | 0 | 1 | 2 | 3 |
| P |  |  | 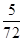 | 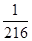 |
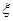 服从二项分布,E
服从二项分布,E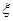 =3×
=3×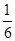 =
=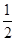 。
。本题考查相互独立事件、互斥事件的概率、离散型随机变量的分布列、二项分布及期望等知识.同时考查利用所学知识分析问题解决问题的能力.
(1)甲、乙、丙三位同学每人是否中奖相互独立,可利用独立事件的概率求解,甲中奖概率为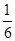 ,乙、丙没有中奖的概率为
,乙、丙没有中奖的概率为 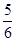 ,相乘即可.
,相乘即可.
(2)中奖人数ξ的所有取值为0,1,2,3,是二项分布.ξ~B(3,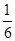 )
)
解(1)P=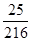 (6分)
(6分)
(2)
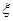 服从二项分布,E
服从二项分布,E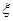 =3×
=3×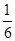 =
=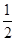 (6分)
(6分)
(1)甲、乙、丙三位同学每人是否中奖相互独立,可利用独立事件的概率求解,甲中奖概率为
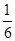 ,乙、丙没有中奖的概率为
,乙、丙没有中奖的概率为 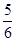 ,相乘即可.
,相乘即可.(2)中奖人数ξ的所有取值为0,1,2,3,是二项分布.ξ~B(3,
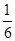 )
)解(1)P=
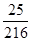 (6分)
(6分)(2)
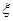 | 0 | 1 | 2 | 3 |
| P |  |  | 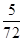 | 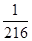 |
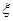 服从二项分布,E
服从二项分布,E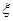 =3×
=3×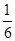 =
=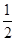 (6分)
(6分)
练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
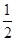 ,乙射击一次中靶概率是
,乙射击一次中靶概率是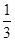 ,
,
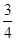
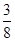
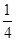
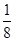
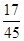
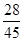
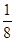
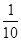
 ,向此平面投掷长为
,向此平面投掷长为 (
( )的针,则此针与任一平行线相交的概率为 。
)的针,则此针与任一平行线相交的概率为 。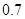 (假定每次通过率相同).
(假定每次通过率相同). 的分布列如下表,则随机变量
的分布列如下表,则随机变量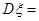 .
.