题目内容
13、异面直线a、b所成的角为80°，过空间一点P作直线l，若l与a、b所成的角都是60°，则这样的直线l共有
4
条．分析：先将异面直线a，b平移到点P，结合图形可知，当使直线在面BPE的射影为∠BPE的角平分线时存在2条满足条件，当直线在面EPD的射影为∠EPD的角平分线时存在2条满足条件，则一共有4条满足条件．
解答：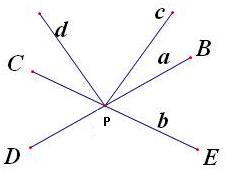
解：先将异面直线a，b平移到点P，则∠BPE=80°，∠EPD=100°
而∠BPE的角平分线与a和b的所成角为40°，
而∠EPD的角平分线与a和b的所成角为50°
∵60°＞40°，60°＞50°
∴直线与a，b所成的角相等且等于60°有且只有4条，
使直线在面BPE的射影为∠BPE的角平分线，
和直线在面EPD的射影为∠EPD的角平分线，
故答案为：4．
解：先将异面直线a，b平移到点P，则∠BPE=80°，∠EPD=100°而∠BPE的角平分线与a和b的所成角为40°，
而∠EPD的角平分线与a和b的所成角为50°
∵60°＞40°，60°＞50°
∴直线与a，b所成的角相等且等于60°有且只有4条，
使直线在面BPE的射影为∠BPE的角平分线，
和直线在面EPD的射影为∠EPD的角平分线，
故答案为：4．
点评：本小题主要考查异面直线所成的角、异面直线所成的角的求法，以及射影等知识，考查空间想象能力、运算能力和推理论证能力，考查转化思想，属于基础题．
练习册系列答案
相关题目
已知两条异面直线a，b所成的角为
，直线l与a，直线l与b所成的角为θ，则θ的范围是（ ）
| π |
| 3 |
A、[
| ||||
B、[
| ||||
C、[
| ||||
D、[
|