题目内容
设异面直线a、b所成的角为
,经过空间一点O有且只有一条直线l与异面直线a、b成等角θ,则θ的值为
或
或
.
| π |
| 3 |
| π |
| 6 |
| π |
| 2 |
| π |
| 6 |
| π |
| 2 |
分析:由已知中异面直线a与b所成的角为60°,设P为空间一点,过P分别作直线a,b的平行线,得到∠APB=60°,过P点作出直线a,b相交所成角的两条角平分线,从而可解.
解答:解:由题意,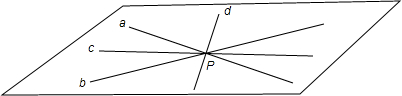 把异面直线a,b平移到相交,使交点为P,
把异面直线a,b平移到相交,使交点为P,
此时∠APB=60°,过P点作直线a,b相交所成角的两条角平分线c,d,如图所示:
则θ为
或
时,经过空间一点O有且只有一条直线l与异面直线a、b成等角θ,
故答案为
或
 把异面直线a,b平移到相交,使交点为P,
把异面直线a,b平移到相交,使交点为P,此时∠APB=60°,过P点作直线a,b相交所成角的两条角平分线c,d,如图所示:
则θ为
| π |
| 6 |
| π |
| 2 |
故答案为
| π |
| 6 |
| π |
| 2 |
点评:本题考查异面直线所成的角,以及解决异面直线所成的角的方法(平移法)的应用,体现了转化的思想和运动变化的思想方法.

练习册系列答案
相关题目