题目内容
（2010•南充一模）已知两异面直线a，b所成的角为
，直线l分别与a，b所成的角都是θ，则θ的取值范围是
| π |
| 3 |
[
，
]
| π |
| 6 |
| π |
| 2 |
[
，
]
．| π |
| 6 |
| π |
| 2 |
分析：先将两异面直线平移到一点，找出两异面直线的所成角，再根据l与a、l与b所成的角都是θ，则l在a′与b′所确定的平面内的射影为a′与b′所成角的平分线，从而可求出θ的取值范围．
解答：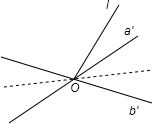
解：先将a与b平移到点O，则a′与b′所成角为
（如图）
l与a、l与b所成的角都是θ，
则l在a′与b′所确定的平面α内的射影为a′与b′所成角的平分线，
当l在平面α内时，θ角最小，为
；
当l与平面α垂直时，θ角最大，为α=
，
∴θ的取值范围是[
，
]，
故答案为[
，
]．
解：先将a与b平移到点O，则a′与b′所成角为| π |
| 3 |
l与a、l与b所成的角都是θ，
则l在a′与b′所确定的平面α内的射影为a′与b′所成角的平分线，
当l在平面α内时，θ角最小，为
| π |
| 6 |
当l与平面α垂直时，θ角最大，为α=
| π |
| 2 |
∴θ的取值范围是[
| π |
| 6 |
| π |
| 2 |
故答案为[
| π |
| 6 |
| π |
| 2 |
点评：本题考查异面直线所成的角，考查空间想象能力、运算能力和推理论证能力．对于异面直线所成的角在求解时，需要把两条异面直线平移到由公共点的位置，从而得到角，本题是一个基础题．
练习册系列答案
相关题目