题目内容
规定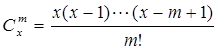 ,其中
,其中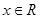 ,
, 是正整数,且
是正整数,且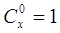 ,这是组合数
,这是组合数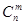 (
( 、
、 是正整数,且
是正整数,且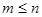 )的一种推广.如当
)的一种推广.如当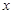 =-5时,
=-5时,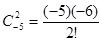
(1)求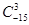 的值;
的值;
(2)设x>0,当x为何值时,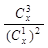 取得最小值?
取得最小值?
(3)组合数的两个性质;
①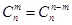 . ②
. ② .
.
是否都能推广到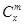 (
(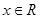 ,
, 是正整数)的情形?若能推广,则写出推广的形式并给出证明;若不能,则说明理由.
是正整数)的情形?若能推广,则写出推广的形式并给出证明;若不能,则说明理由.
(1)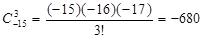 ; (2)当
; (2)当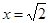 时,
时,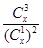 取得最小值;(3)性质②能推广,它的推广形式是
取得最小值;(3)性质②能推广,它的推广形式是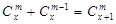 ,
,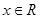 ,
, 是正整数.
是正整数.
解析试题分析:(1)利用类比法即可求解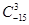 =
=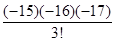 =-680为多少,(2)先求得关于x的解析式
=-680为多少,(2)先求得关于x的解析式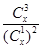
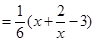 ,然后利用基本不等式求解;(3)考察的是大家对排列组合的理解和应用.
,然后利用基本不等式求解;(3)考察的是大家对排列组合的理解和应用.
试题解析:(1)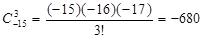
(2)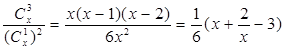 6分
6分
∵ x > 0 , 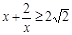 当且仅当
当且仅当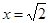 时,等号成立.
时,等号成立.
∴ 当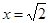 时,
时,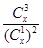 取得最小值. 8分
取得最小值. 8分
(3)性质①不能推广,例如当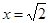 时,
时,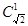 有定义,但
有定义,但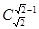 无意义; 10分
无意义; 10分
性质②能推广,它的推广形式是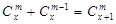 ,
,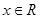 ,
, 是正整数. 12分
是正整数. 12分
事实上,当m=1时,有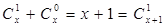 .
.
当m≥2时.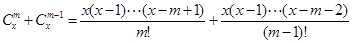
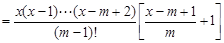
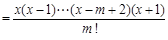
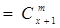 . 14分
. 14分
考点:1,排列的公式2,基本不等式,3,规纳总结方法的应用.

练习册系列答案
 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
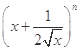 的展开式中前三项的系数成等差数列.
的展开式中前三项的系数成等差数列.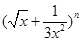 的第五项的二项式系数与第三项的二项式系数的比是
的第五项的二项式系数与第三项的二项式系数的比是 ,
, 的展开式的二项式系数的和比(3x-1)n的展开式的二项式系数和大992,求(2x-
的展开式的二项式系数的和比(3x-1)n的展开式的二项式系数和大992,求(2x-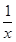 )2n的展开式中,(1)二项式系数最大的项;(2)系数的绝对值最大的项.
)2n的展开式中,(1)二项式系数最大的项;(2)系数的绝对值最大的项.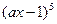 的展开式中
的展开式中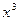 的系数是80,则实数
的系数是80,则实数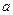 的值是 .
的值是 .