题目内容
(12分)已知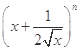 的展开式中前三项的系数成等差数列.
的展开式中前三项的系数成等差数列.
(1)求n的值; (2)求展开式中系数最大的项.
(1)8;(2)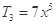 ,
,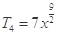
解析试题分析:(1)由已知有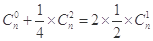 即
即 ,解得n=8,n=1(舍去);(2)由(1)知n=8,设第r+1的系数最大,则
,解得n=8,n=1(舍去);(2)由(1)知n=8,设第r+1的系数最大,则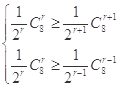 即
即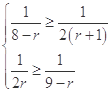 ,解得r=2或r=3, 所以系数最大的项为
,解得r=2或r=3, 所以系数最大的项为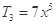 ,
,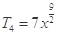 .
.
试题解析:(1)由题设,得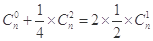 , 即
, 即 ,
,
解得n=8,n=1(舍去).
(2)设第r+1的系数最大,则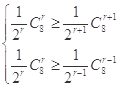 即
即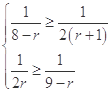
解得r=2或r=3.
所以系数最大的项为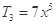 ,
,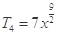 .
.
考点:二项式定理及其性质

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
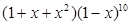 展开式中
展开式中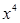 的系数为______.
的系数为______.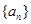 为
为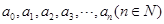 ,
,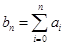 表示
表示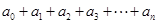 ,
,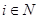 .
.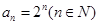 ,求
,求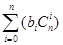 ;
;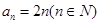 ,求
,求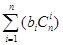 .
.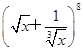 的展开式中二项式系数最大项.
的展开式中二项式系数最大项.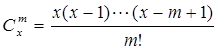 ,其中
,其中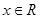 ,
, 是正整数,且
是正整数,且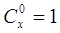 ,这是组合数
,这是组合数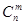 (
( 是正整数,且
是正整数,且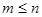 )的一种推广.如当
)的一种推广.如当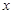 =-5时,
=-5时,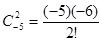
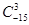 的值;
的值;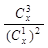 取得最小值?
取得最小值?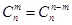 . ②
. ② .
.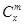 (
(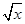 )n的展开式中,某一项的系数恰好是它前一项系数的2倍,而且是它后一项系数的
)n的展开式中,某一项的系数恰好是它前一项系数的2倍,而且是它后一项系数的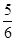 ,求展开式中二项式系数最大的项.
,求展开式中二项式系数最大的项.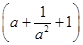 10展开式中的常数项.
10展开式中的常数项.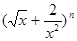 展开式中只有第六项的二项式系数最大,则展开式中的常数项等于 .
展开式中只有第六项的二项式系数最大,则展开式中的常数项等于 .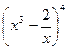 的展开式中的常数项等于 ;
的展开式中的常数项等于 ;