题目内容
【题目】设
的内角A，B，C的对边长a，b，c成等比数列，
，延长BC至D，若
，则
面积的最大值为（ ）
A.2B.
C.
D.
【答案】B
【解析】
由两角和、差的余弦和正弦定理可得：
为正三角形，设
，由基本不等式得：S△ACD＝
＝
＝
（当且仅当x＝2﹣x即x＝1时取等号）得解．
因为
，所以
，所以
，①
因为a，b，c成等比数列，所以b2＝ac，由正弦定理得：sin2B＝sinAsinC，②
①﹣②得：
，
化简得：4cos2B+4cosB﹣3＝0，解得：cosB＝
或cosB＝
（舍），又0＜B＜π，所以B＝
，
①+②：
，
cos（A﹣C）＝1，即A﹣C＝0，即A＝C，即三角形ABC为正三角形，
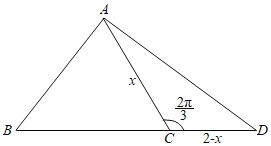
如图所示，设，则
，由已知得0＜x＜2，则S△ACD＝＝＝（当且仅当x＝2﹣x，即x＝1时取等号）
故选：B
练习册系列答案
阅读快车系列答案
相关题目
