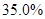题目内容
(本小题满分15分)因发生意外交通事故,一辆货车上的某种液体泄漏到一渔塘中.为了治污,根据环保部门的建议,现决定在渔塘中投放一种可与污染液体发生化学反应的药剂.已知每投放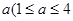 ,且
,且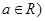 个单位的药剂,它在水中释放的浓度
个单位的药剂,它在水中释放的浓度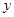 (克/升)随着时间
(克/升)随着时间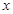 (天)变化的函数关系式近似为
(天)变化的函数关系式近似为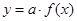 ,其中
,其中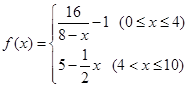 .
.
若多次投放,则某一时刻水中的药剂浓度为每次投放的药剂在相应时刻所释放的浓度之和.根据经验,当水中药剂的浓度不低于4(克/升)时,它才能起到有效治污的作用.
(1)若一次投放4个单位的药剂,则有效治污时间可达几天?
(2)若第一次投放2个单位的药剂,6天后再投放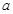 个单位的药剂,要使接下来的4天中能够持续有效治污,试求
个单位的药剂,要使接下来的4天中能够持续有效治污,试求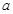 的最小值.(精确到0.1,参考数据:
的最小值.(精确到0.1,参考数据: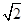 取1.4)
取1.4)
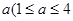 ,且
,且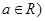 个单位的药剂,它在水中释放的浓度
个单位的药剂,它在水中释放的浓度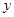 (克/升)随着时间
(克/升)随着时间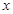 (天)变化的函数关系式近似为
(天)变化的函数关系式近似为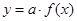 ,其中
,其中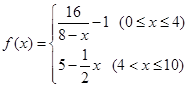 .
.若多次投放,则某一时刻水中的药剂浓度为每次投放的药剂在相应时刻所释放的浓度之和.根据经验,当水中药剂的浓度不低于4(克/升)时,它才能起到有效治污的作用.
(1)若一次投放4个单位的药剂,则有效治污时间可达几天?
(2)若第一次投放2个单位的药剂,6天后再投放
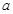 个单位的药剂,要使接下来的4天中能够持续有效治污,试求
个单位的药剂,要使接下来的4天中能够持续有效治污,试求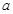 的最小值.(精确到0.1,参考数据:
的最小值.(精确到0.1,参考数据: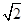 取1.4)
取1.4)(1)因为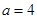 ,所以
,所以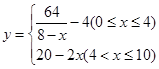
则当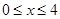 时,由
时,由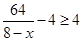 ,解得
,解得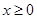 ,所以此时
,所以此时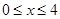 ;
;
当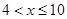 时,由
时,由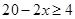 ,解得
,解得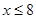 ,所以此时
,所以此时 .
.
综合,得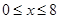 ,若一次投放4个单位的制剂,则有效治污时间可达8天.
,若一次投放4个单位的制剂,则有效治污时间可达8天.
(2)当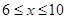 时,
时,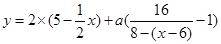
= =
= ,因为
,因为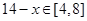 ,而
,而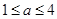 ,
,
所以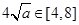 ,故当且仅当
,故当且仅当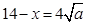 时,y有最小值为
时,y有最小值为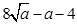 令
令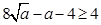 ,解得
,解得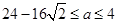 ,所以
,所以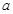 的最小值为
的最小值为
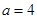 ,所以
,所以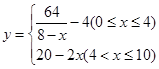
则当
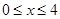 时,由
时,由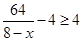 ,解得
,解得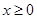 ,所以此时
,所以此时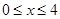 ;
;当
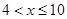 时,由
时,由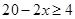 ,解得
,解得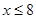 ,所以此时
,所以此时 .
.综合,得
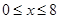 ,若一次投放4个单位的制剂,则有效治污时间可达8天.
,若一次投放4个单位的制剂,则有效治污时间可达8天.(2)当
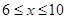 时,
时,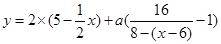
=
 =
= ,因为
,因为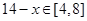 ,而
,而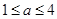 ,
,所以
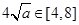 ,故当且仅当
,故当且仅当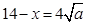 时,y有最小值为
时,y有最小值为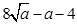 令
令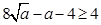 ,解得
,解得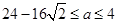 ,所以
,所以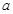 的最小值为
的最小值为
略

练习册系列答案
 优等生题库系列答案
优等生题库系列答案 53天天练系列答案
53天天练系列答案
相关题目
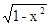 =k(x-2)+1有两解则k的取值范围是
=k(x-2)+1有两解则k的取值范围是  ,其中e是自然数的底数,
,其中e是自然数的底数, 。
。 时,解不等式
时,解不等式 ;
; 在[-1,1]上是单调增函数,求
在[-1,1]上是单调增函数,求 的取值范围;
的取值范围; 时,求整数k的所有值,使方程
时,求整数k的所有值,使方程 在[k,k+1]上有解。
在[k,k+1]上有解。 格为30元,浮动价格(单位:元)与销售量(单位:万套)成反比,比例系数为l0.假设不计其它成本,即销售每套丛书的利润 = 售价 一 供货价格.问:
格为30元,浮动价格(单位:元)与销售量(单位:万套)成反比,比例系数为l0.假设不计其它成本,即销售每套丛书的利润 = 售价 一 供货价格.问: 书定价为100元时,书商能获得的总利润是多少万元?
书定价为100元时,书商能获得的总利润是多少万元? 的定义域是一切实数
的定义域是一切实数 ,且
,且 ,求
,求 的值”。请问
的值”。请问 (元)与月处理量
(元)与月处理量 (吨)之间的函数关系式可近似的表示为:
(吨)之间的函数关系式可近似的表示为: ,且每处理一吨二氧化碳得到可利用的化工产品价值为300元。
,且每处理一吨二氧化碳得到可利用的化工产品价值为300元。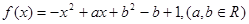 ,对任意实数
,对任意实数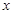 都有
都有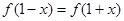 成立,若当
成立,若当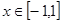 时,
时,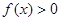 恒成立,则
恒成立,则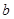 的取值范围是
的取值范围是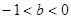


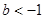
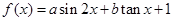 ,且
,且 则
则 ___________
___________