题目内容
如图,在直三棱柱ABC-A1B1C1中,平面A1BC⊥侧面A1ABB1.
(Ⅰ)求证:AB⊥BC;
(Ⅱ)若直线AC与平面A1BC所成的角为θ,二面角A1-BC-A的大小为φ,试判断θ与φ的大小关系,并予以证明.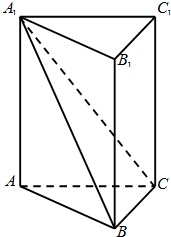
(Ⅰ)求证:AB⊥BC;
(Ⅱ)若直线AC与平面A1BC所成的角为θ,二面角A1-BC-A的大小为φ,试判断θ与φ的大小关系,并予以证明.

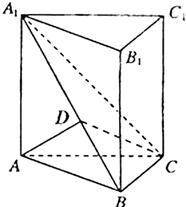
(Ⅰ)证明:如图,过点A在平面A1ABB1内作AD⊥A1B于D,
由平面A1BC⊥侧面A1ABB1,且平面A1BC∩侧面A1ABB1=A1B,得
AD⊥平面A1BC,又BC?平面A1BC,
所以AD⊥BC.
因为三棱柱ABC-A1B1C1是直三棱柱,
则AA1⊥底面ABC,
所以AA1⊥BC.
又AA1∩AD=A,从而BC⊥侧面A1ABB1,
又AB?侧面A1ABB1,故AB⊥BC.
(Ⅱ)解法1:连接CD,则由(Ⅰ)知∠ACD是直线AC与平面A1BC所成的角,∠ABA1是二面角A1-BC-A的平面角,即∠ACD=θ,∠ABA1=φ,
于是在Rt△ADC中,sinθ=
| AD |
| AC |
| AD |
| AB |
由AB<AC,得sinθ<sinφ,又0<θ,φ<
| π |
| 2 |
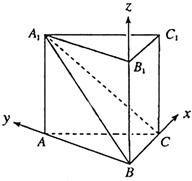
解法2:由(Ⅰ)知,以点B为坐标原点,以BC、BA、BB1所在的直线分
别为x轴、y轴、z轴,建立如图所示的空间直角坐标系,
设AA1=a,AC=b,
AB=c,则B(0,0,0),A(0,c,0),C(
| b2-c2 |
于是
| BC |
| b2-c2 |
| BA1 |
| AC |
| b2-c2 |
| AA1 |
设平面A1BC的一个法向量为n=(x,y,z),
则由
|
|
可取n=(0,-a,c),于是n•
| AC |
| AC |
n•
| ||
|n|•|
|
| ac | ||
b
|
| ||||
|
|
| c | ||
|
所以sinφ=
| a | ||
|
于是由c<b,得
| ac | ||
b
|
| a | ||
|
即sinθ<sinφ,又0<θ,φ<
| π |
| 2 |

练习册系列答案
相关题目




