题目内容
设向量i=(1,0),j=(0,1),a=xi+(y+2)j,b=xi+(y-2)j且|a|+|b|=8,x、y∈R.(1)求动点P(x,y)的轨迹方程;
(2)过点M(0,3),作直线l与曲线C交于A,B两点,设ON=OA+OB,问是否存在直线l,使得四边形OANB为矩形?若存在,求出l的方程;若不存在,请说明理由.
解:(1)∵i=(1,0),j=(0,1),|a|+|b|=8,∴![]() =8,
=8,
即点P(x, y)到点(0,—2)与点(0,2)的距离之和为8.
设F1(0,—2),F2(0,2),∴|F 1F2|=4,|PF1|+|PF2|=8>|F1F2|,
由椭圆定义知点P的轨迹C是以F1.F2为焦点的椭圆.
∵2a=8, 2c=4,∴a=4, c=2,∴b2=a2—c2=12,
∴所求轨迹C方程为![]() =1.
=1.
(2)∵![]() ,∴OANB是平行四边形.
,∴OANB是平行四边形.
∵l过点M(0,3),若l是y轴,则A,B是椭圆的顶点,此时![]() =0,
=0,
∴N与O重合,这与四边形是平行四边形矛盾.所以直线l的斜率k必存在.
设直线l的方程为y=kx+3,A(x1,y1),B(x2,y2),
若存在直线l使得OANB是矩形,则,OA![]() OB∴
OB∴![]() =0,即x1x2+y 1y2=0.
=0,即x1x2+y 1y2=0.
而y1y2=(kx1+3)(kx2+3)=k2x1x2+3k(x1+x2)+9,
∴(1+k2)x1x2+3k(x1+x2)+9=0①
由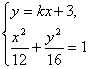 消去y,得(3k2+4)x2+18kx—21=0②
消去y,得(3k2+4)x2+18kx—21=0②
∵Δ=(18k)2—4(3k2+4)(—21)=(18k)2+84(3k2+4)>0,
∴方程②必有两实根x1.x2,且x1+x2=![]() ,x1x2=
,x1x2=![]() ,代入①得,
,代入①得,
-(1+k2)![]() =0,解得k2=
=0,解得k2=![]() ,
,
∴k=±![]() .所以存在符合题意的直线l,其方程为:
.所以存在符合题意的直线l,其方程为:
y=![]() 或y=
或y=![]() x+3.
x+3.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目