题目内容
已知向量
=(1,0),
=(0,1),设与2
+
同向的单位向量为
,向量
-3
与向量
的夹角为θ,则下列说法正确的是( )
| i |
| j |
| i |
| j |
| e |
| j |
| i |
| i |
分析:由题意可得:2
+
的坐标,进而可得其模长,故可得其单位向量,后面由夹角公式即可得解.
| i |
| j |
解答:解:由题意可得:2
+
=2(1,0)+(0,1)=(2,1),
由模长公式可得其模长为:
=
,
故其单位向量
=
(2,1)=(
,
);
又向量
-3
=(-3,1),向量
=(1,0),
由夹角公式可得cosθ=
=
=-
故选B
| i |
| j |
由模长公式可得其模长为:
| 22+12 |
| 5 |
故其单位向量
| e |
| 1 | ||
|
2
| ||
| 5 |
| ||
| 5 |
又向量
| j |
| i |
| i |
由夹角公式可得cosθ=
(
| ||||||
|
|
| -3 | ||
|
3
| ||
| 10 |
故选B
点评:本题考查向量的单位向量和向量的夹角公式,属中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
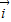 =(1,0),
=(1,0),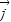 =(0,1),
=(0,1),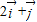 垂直的向量是( )
垂直的向量是( )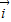 =(1,0),
=(1,0), =(0,1),
=(0,1),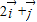 垂直的向量是( )
垂直的向量是( )