题目内容
设函数f(x)=x![]() +
+![]() ,A0为坐标原点,An为函数y=f(x)图象上横坐标为
,A0为坐标原点,An为函数y=f(x)图象上横坐标为
n(n∈N*)的点,向量an=![]() ,向量i=(1,0),设θn为向量an与向量i的夹角,满足
,向量i=(1,0),设θn为向量an与向量i的夹角,满足![]() tanθk<
tanθk<![]() 的最大整数n是( )
的最大整数n是( )
A.2 B.3 C.4 D.5
B.由已知得An![]() ,
,
又an=![]() =
=![]() =
=![]() ,
,
tanθn=![]() =
=![]() =
=![]() +
+![]() ,
,
所以![]() tanθk=
tanθk=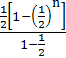 +
+![]()
=2-![]() -
-![]() ,
,
验证知n=3符合![]() tanθk<
tanθk<![]() .
.

练习册系列答案
相关题目
题目内容
设函数f(x)=x![]() +
+![]() ,A0为坐标原点,An为函数y=f(x)图象上横坐标为
,A0为坐标原点,An为函数y=f(x)图象上横坐标为
n(n∈N*)的点,向量an=![]() ,向量i=(1,0),设θn为向量an与向量i的夹角,满足
,向量i=(1,0),设θn为向量an与向量i的夹角,满足![]() tanθk<
tanθk<![]() 的最大整数n是( )
的最大整数n是( )
A.2 B.3 C.4 D.5
B.由已知得An![]() ,
,
又an=![]() =
=![]() =
=![]() ,
,
tanθn=![]() =
=![]() =
=![]() +
+![]() ,
,
所以![]() tanθk=
tanθk=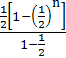 +
+![]()
=2-![]() -
-![]() ,
,
验证知n=3符合![]() tanθk<
tanθk<![]() .
.
