题目内容
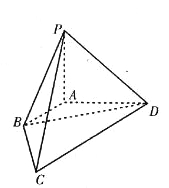
【题目】如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,AB=2AD=2,∠DAB=60°,PA=PC=2,且平面ACP⊥平面ABCD.
(Ⅰ)求证:CB⊥PD;
(Ⅱ)求二面角C-PB-A的余弦值.
【答案】(1)见证明;(2) ![]()
【解析】
(1)证明PO⊥平面ABCD得出PO⊥BC,利用勾股定理证明![]() ,从而BC⊥平面PBD,于是BC⊥PD;
,从而BC⊥平面PBD,于是BC⊥PD;
(2)建立空间坐标系,求出平面PAB和平面PBC的法向量,通过计算法向量的夹角得出二面角的大小.
解:(1)连![]() ,
,![]() 交于点
交于点![]() ,连
,连![]()
由平面![]() ,平面
,平面![]() .
.
又![]()
![]()
又![]()
![]()
又![]()
![]()
![]() ,
,
又![]()
![]()
![]()
![]()
(2)由(1)知![]() ,以
,以![]() 为坐标原点,
为坐标原点,![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴,过点
轴,过点![]() 与平面
与平面![]() 垂直的直线为
垂直的直线为![]() 轴建立如图所示的空间直角坐标系.
轴建立如图所示的空间直角坐标系.
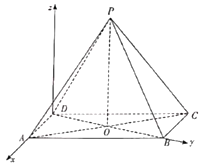
由(1)知![]() ,则
,则![]() 轴.
轴.
由平面几何知识易得![]() ,
,
则![]()
于是![]() ,
,
设平面![]() 的法向量为
的法向量为![]() .
.
则![]() ,即
,即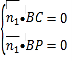 ,
,
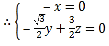 取
取![]() ,则
,则![]() ,则
,则![]()
同理可求得平面![]() 的一个向量
的一个向量![]()
于是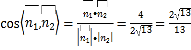
分析知二角面![]() 的余弦值为
的余弦值为![]() .
.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
【题目】手机给人们的生活带来便捷,但同时也对中学生的生活和学习造成了严重的影响,某校高一几个学生成立研究性学习小组,就使用手机对学习成绩的影响随机抽取了该校100名学生的期末考试成绩并制成如下的表,则下列说法正确的是( )
成绩优秀 | 成绩不优秀 | 合计 | |
不用手机 | 40 | 10 | 50 |
使用手机 | 5 | 45 | 50 |
合计 | 45 | 55 | 100 |
(附:![]() 列联表
列联表![]() 公式:
公式: ,其中
,其中![]() )
)
| 0.010 | 0.005 | 0.001 |
| 6.635 | 7.879 | 10.828 |
A.在犯错误的概率不超过0.001的前提下认为使用手机与学习成绩有关.
B.在犯错误的概率不超过0.001的前提下认为使用手机与学习成绩无关.
C.有![]() 的把握认为使用手机对学习成绩无影响.
的把握认为使用手机对学习成绩无影响.
D.无![]() 的把握认为使用手机对学习成绩有影响.
的把握认为使用手机对学习成绩有影响.