题目内容
设有关于x的一元二次方程x2+2ax+b2=0.
(1)若a是从0,1,2,3四个数中任取的一个数,b是从0,1,2三个数中任取的一个数,求方程有实根的概率.
(2)若a是从区间[0,t+1]任取的一个数,b是从区间[0,t]任取的一个数,其中t满足2≤t≤3,求方程有实根的概率,并求出其概率的最大值.
(1)若a是从0,1,2,3四个数中任取的一个数,b是从0,1,2三个数中任取的一个数,求方程有实根的概率.
(2)若a是从区间[0,t+1]任取的一个数,b是从区间[0,t]任取的一个数,其中t满足2≤t≤3,求方程有实根的概率,并求出其概率的最大值.
分析:(1)由题意知本题是一个古典概型,试验发生包含的基本事件共12个,然后找出满足x2+2ax+b2=0有实数根即a≥b
的基本事件,根据古典概型的概率公式即可即可;
(2)a,b构成的实数对(a,b)满足条件有0≤a≤t+1,0≤b≤t,a≥b,设事件B为“方程有实根”,则此事件满足几何概型,利用几何概型的概率公式进行计算即可.
的基本事件,根据古典概型的概率公式即可即可;
(2)a,b构成的实数对(a,b)满足条件有0≤a≤t+1,0≤b≤t,a≥b,设事件B为“方程有实根”,则此事件满足几何概型,利用几何概型的概率公式进行计算即可.
解答:解:设事件A为“方程有实根”,x2+2ax+b2=0有实数根需满足△=4a2-4b2≥0,即a2≥b2.
又a≥0,b≥0,所以a≥b
(1)由题意知本题是一个古典概型,试验发生包含的基本事件共12个:
(0,0)(0,1)(0,2)(1,0)(1,1)(1,2)(2,0)(2,1)(2,2)(3,0)(3,1)(3,2)
其中第一个数表示a的取值,第二个数表示b的取值.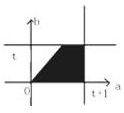
事件A中包含9个基本事件,(0,0)(1,0)(1,1)(2,0)(2,1)(2,2)(3,0)(3,1)(3,2)
∴事件A发生的概率为P=
=
(2)a,b构成的实数对(a,b)满足条件有0≤a≤t+1,0≤b≤t,a≥b,如图
设事件B为“方程有实根”,则此事件满足几何概型
P(B)=
=
=
=
[1+
]
因为2≤t≤3,所以3≤t+1≤4,即
≤
≤
所以
≤1+
≤
即
≤P(B)≤
又a≥0,b≥0,所以a≥b
(1)由题意知本题是一个古典概型,试验发生包含的基本事件共12个:
(0,0)(0,1)(0,2)(1,0)(1,1)(1,2)(2,0)(2,1)(2,2)(3,0)(3,1)(3,2)
其中第一个数表示a的取值,第二个数表示b的取值.

事件A中包含9个基本事件,(0,0)(1,0)(1,1)(2,0)(2,1)(2,2)(3,0)(3,1)(3,2)
∴事件A发生的概率为P=
| 9 |
| 12 |
| 3 |
| 4 |
(2)a,b构成的实数对(a,b)满足条件有0≤a≤t+1,0≤b≤t,a≥b,如图
设事件B为“方程有实根”,则此事件满足几何概型
P(B)=
| S阴影 |
| S矩形 |
| ||
| t(t+1) |
| t+2 |
| 2(t+1) |
| 1 |
| 2 |
| 1 |
| t+1 |
因为2≤t≤3,所以3≤t+1≤4,即
| 1 |
| 4 |
| 1 |
| t+1 |
| 1 |
| 3 |
所以
| 5 |
| 4 |
| 1 |
| t+1 |
| 4 |
| 3 |
| 5 |
| 8 |
| 2 |
| 3 |
点评:本题主要考查了列举法计算基本事件数及事件发生的概率,以及几何概型的概率,同时考查了画图的能力,属于中档题.

练习册系列答案
相关题目