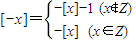题目内容
设x∈R,用[x]表示不超过x的最大值整数,则y=[x]称为高斯函数,下列关于高斯函数的说法正确的有
①[-x]=-[x]
②x-1<[x]≤x
③?x,y∈R,[x]+[y]≤[x+y]
④?x≥0,y≥0,[xy]≤[x][y]
⑤离实数x最近的整数是-[-x+
].
①[-x]=-[x]
②x-1<[x]≤x
③?x,y∈R,[x]+[y]≤[x+y]
④?x≥0,y≥0,[xy]≤[x][y]
⑤离实数x最近的整数是-[-x+
| 1 | 2 |
分析:根据高斯函数的定义,分别进行判断即可.
解答:解:①若x=
,则[-x]═[-
]=-1,[x]=[
]=0,∴①错误.
②若x是整数,则[x]=x,此时不等式x-1<[x]≤x成立,
若x不是整数,则根据定义可知[x]<x,且[x]>x-1,
此时不等式x-1<[x]≤x,成立,∴②正确.
③?x,y∈R,x-1<[x]≤x,y-1<[y]≤y,
x+y-1<[x+y]≤x+y,
若x,y至少含有一个整数,则,[x]+[y]=[x+y]成立.
若x,y都不是整数,则[x]+[y]<[x+y],
综上:[x]+[y]≤[x+y],∴③正确.
④?x≥0,y≥0,
当x=
,y=4时,[x]=0,[y]=4,xy=2,
即[xy]=2,此时,[xy]≤[x][y]不成立,
∴④错误.
⑤∵-[-x+
]=[x-
],则根据高斯函数的定义可知,而此时离实数最近的整数是1,
若m-
<x≤m+
,(其中m为整数),则m叫做离实数x最近的整数,
则m-1<x-
≤m,
∴,离实数x最近的整数是m=[x-
].
故⑤正确.
故答案为:②③⑤
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
②若x是整数,则[x]=x,此时不等式x-1<[x]≤x成立,
若x不是整数,则根据定义可知[x]<x,且[x]>x-1,
此时不等式x-1<[x]≤x,成立,∴②正确.
③?x,y∈R,x-1<[x]≤x,y-1<[y]≤y,
x+y-1<[x+y]≤x+y,
若x,y至少含有一个整数,则,[x]+[y]=[x+y]成立.
若x,y都不是整数,则[x]+[y]<[x+y],
综上:[x]+[y]≤[x+y],∴③正确.
④?x≥0,y≥0,
当x=
| 1 |
| 2 |
即[xy]=2,此时,[xy]≤[x][y]不成立,
∴④错误.
⑤∵-[-x+
| 1 |
| 2 |
| 1 |
| 2 |
若m-
| 1 |
| 2 |
| 1 |
| 2 |
则m-1<x-
| 1 |
| 2 |
∴,离实数x最近的整数是m=[x-
| 1 |
| 2 |
故⑤正确.
故答案为:②③⑤
点评:本题主要考查高斯函数的定义及应用,正确理解题意是解决本题的关键,综合性较强,难度较大.

练习册系列答案
相关题目