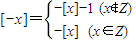题目内容
设x∈R,用[x]表示不超过x的最大整数,例如[-1.5]=-2,[5.1]=5.则下列对函数f(x)=[x]所具有的性质说法正确的有
|
分析:根据[x]表示不超过x的最大整数可知[x]的结果为整数则值域为Z,所以①正确;因为[x]表示不超过x的最大整数,当x1≤x2,则[x1]≤[x2],②正确;如果n为Z则[n+x]=n+[x],故③正确;根据定义知:[x]≤x<[x]+1;当x是整数时[-x]=-[x],当x不是整数时,[-x]=-[x]-1.
解答:解:因为[x]表示不超过x的最大整数,可知[x]的结果为整数,所以值域为Z,①正确;
因为[x]表示不超过x的最大整数,当x1≤x2,则[x1]≤[x2],②正确;
如果n为Z则[n+x]=n+[x],故③正确;根据定义知:[x]≤x<[x]+1,故④正确;x属于整数时,[-x]=-[x],
当x不是整数时,[-x]=-[x]-1.是一个分段函数,故⑤正确.
故答案为①②③④⑤
因为[x]表示不超过x的最大整数,当x1≤x2,则[x1]≤[x2],②正确;
如果n为Z则[n+x]=n+[x],故③正确;根据定义知:[x]≤x<[x]+1,故④正确;x属于整数时,[-x]=-[x],
当x不是整数时,[-x]=-[x]-1.是一个分段函数,故⑤正确.
故答案为①②③④⑤
点评:考查学生理解函数定义域及求法的能力,求函数值域的能力,及理解掌握分段函数的能力.

练习册系列答案
相关题目