题目内容
已知平面上直线l的方向向量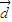
=（3，-4），点O（0，0）和A（4，-2）l上的射影分别是O1和A1，则|
|= ．
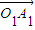【答案】分析：由已知中面上直线l的方向向量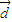
=（3，-4），点O（0，0）和A（4，-2），我们易计算出直线l及直线OA的斜率，进而可求出直线OA与直线l的夹角为θ的余弦值，进而根据
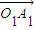|=|OA|•cosθ得到答案．
解答：解：∵平面上直线l的方向向量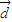
=（3，-4），
∴直线l的斜率k=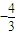
又∵O（0，0）和A（4，-2）
∴直线OA的斜率k′=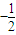
|OA|=2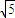
设直线OA与直线l的夹角为θ
则tanθ=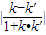
=
=
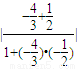则cosθ=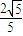
∴|
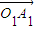|=|OA|•cosθ=2
•
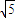=4
故答案为：4
点评：本题考查的知识点是直线的斜率，直线的夹角到直线到直线的角，其中利用tanθ=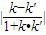
计算出两直线的夹角，及|
|=|OA|•cosθ是解答本题的关键．
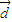=（3，-4），点O（0，0）和A（4，-2），我们易计算出直线l及直线OA的斜率，进而可求出直线OA与直线l的夹角为θ的余弦值，进而根据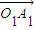|=|OA|•cosθ得到答案．解答：解：∵平面上直线l的方向向量
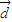=（3，-4），∴直线l的斜率k=
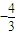
又∵O（0，0）和A（4，-2）
∴直线OA的斜率k′=
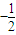
|OA|=2
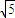
设直线OA与直线l的夹角为θ
则tanθ=
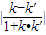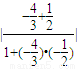==则cosθ=
∴|
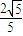
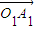|=|OA|•cosθ=2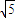•=4故答案为：4
点评：本题考查的知识点是直线的斜率，直线的夹角到直线到直线的角，其中利用tanθ=
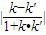计算出两直线的夹角，及||=|OA|•cosθ是解答本题的关键． 
练习册系列答案
相关题目
已知平面上直线l的方向向量
=（-
，
），点O（0，0）和A（1，-2）在l上的射影分别是O'和A′，则
=λ
，其中λ等于（ ）
| e |
| 4 |
| 5 |
| 3 |
| 5 |
| O′A′ |
| e |
A、
| ||
B、-
| ||
| C、2 | ||
| D、-2 |
已知平面上直线l的方向向量
=(
，-
)，点O（0，0）和P（-2，2）在直线l的正射影分别是O'和P'，且
=λ
，则λ等于（ ）
| e |
| ||
| 2 |
| 1 |
| 2 |
| O′P′ |
| e |
A、-2(
| ||
B、2(
| ||
C、-(
| ||
D、
|
)，点O(0,0)和A(1,-2)在l上的射影分别是O1、A1，则
=λe，其中λ等于( )
B.
C.2 D.-2