题目内容
已知平面上直线l的方向向量e=(
)，点O(0,0)和A(1,-2)在l上的射影分别是O1、A1，则
=λe，其中λ等于( )A.
B.
C.2 D.-2
解析：方法一：由向量在已知向量上的射影的定义知
λ=||cos〈e，〉==·
=
-
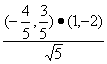=-2.
方法二：利用数形结合的思想，作图可得.令向量e过原点,故
与e方向相反.排除A、C，检验B、D可知D正确.
答案：D
练习册系列答案
同步练习强化拓展系列答案
相关题目
已知平面上直线l的方向向量
=（-
，
），点O（0，0）和A（1，-2）在l上的射影分别是O'和A′，则
=λ
，其中λ等于（ ）
| e |
| 4 |
| 5 |
| 3 |
| 5 |
| O′A′ |
| e |
A、
| ||
B、-
| ||
| C、2 | ||
| D、-2 |
已知平面上直线l的方向向量
=(
，-
)，点O（0，0）和P（-2，2）在直线l的正射影分别是O'和P'，且
=λ
，则λ等于（ ）
| e |
| ||
| 2 |
| 1 |
| 2 |
| O′P′ |
| e |
A、-2(
| ||
B、2(
| ||
C、-(
| ||
D、
|