题目内容

设m，n是不同的直线，α，β，γ是不同的平面，有以下四个命题：
①
α∥β
α∥γ
?β∥γ
②
α⊥β
m∥α
?m⊥β
③
m⊥α
m∥β
?α⊥β
④
m∥n
n?α
?m∥α
其中，真命题是（　　）
A、①④B、②③C、①③D、②④
分析：对每一选支进行逐一判定，不正确的只需取出反例，正确的证明一下即可．
解答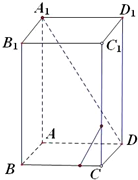：精英家教网解：
对于①利用平面与平面平行的性质定理可证α∥β，α∥γ，则β∥γ，正确
对于②面BD⊥面D1C，A1B1∥面BD，此时A1B1∥面D1C，不正确
对应③∵m∥β∴β内有一直线与m平行，而m⊥α，
根据面面垂直的判定定理可知α⊥β，故正确
对应④m有可能在平面α内，故不正确，
故选C
点评：本题主要考查了平面与平面之间的位置关系，以及空间中直线与平面之间的位置关系，考查空间想象能力、运算能力和推理论证能力，属于基础题．
练习册系列答案
相关题目
8、设m、n是不同的直线，α、β、γ是不同的平面，有以下四个命题：①若α∥β，α∥γ，则β∥γ②若α⊥β，m∥α，则m⊥β③若m⊥α，m∥β，则α⊥β④若m∥n，?n?α，则m∥α其中真命题的序号是（　　）
4、设m，n是不同的直线，是不同的平面，则下列四个命题：①若α∥β，m?α，则m∥β，②若m∥α，n?α，则m∥n，③若α⊥β，m∥α，则m⊥β，④若m⊥α，m∥β，则α⊥β
其中正确的是（　　）
6、设m、n是不同的直线，α、β、γ是不同的平面，有以下四个命题：
（1）若n∥α，m∥β，α∥β，则n∥m；   （2）若m⊥α，n∥α，则m⊥n
（3）若α⊥γ，β⊥γ，则α∥β；         （4）若α∥β，β∥γ，m⊥α，则m⊥γ
其中真命题的个数是（　　）
设m、n是不同的直线，α、β、γ是不同的平面，有以下四个命题：
（1）
α∥β
α∥γ
?β∥γ；
（2）
α⊥β
m∥α
?m⊥β；
（3）
m⊥α
m∥β
?α⊥β；
（4）
m∥n
n?α
?m∥α．
其中，假命题是（　　）
A、（1）（2）
B、（2）（3）
C、（1）（3）
D、（2）（4）
设m、n是不同的直线，α、β是不同的平面，有以下四个命题：
①若m⊥α，n⊥α，则m∥n； 
②若α⊥β，m∥α，则m⊥β；
③若m上α，m⊥n，则n∥α；    
④若n⊥α，n⊥β，则β∥α．
其中，真命题的序号是（　　）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网