题目内容
(2012•汕头一模)有以下四个命题:
①△ABC中,“A>B”是“sinA>sinB”的充要条件;
②若命题p:?x∈R,sinx≤1,则?p:?x∈R,sinx>1;
③不等式10x>x2在(0,+∞)上恒成立;
④设有四个函数y=x-1,y=x
,y=x
,y=x3,其中在(0,+∞)上是增函数的函数有3个.
其中真命题的序号是( )
①△ABC中,“A>B”是“sinA>sinB”的充要条件;
②若命题p:?x∈R,sinx≤1,则?p:?x∈R,sinx>1;
③不等式10x>x2在(0,+∞)上恒成立;
④设有四个函数y=x-1,y=x
| 1 |
| 2 |
| 1 |
| 3 |
其中真命题的序号是( )
分析:三角形中,大边对大角以及正弦定理得到“A>B”?a>b?2RsinA>2RsinB?sinA>sinB,判定出①正确;
根据含量词的命题的否定规则判定出②不正确;
通过构造函数,根据导函数的正负与函数单调性的关系求出y=10x-x2>1,进一步能判定出③正确;
根据5个常见幂函数的图象得到函数y=x-1在(0,+∞)上是函减数;函数y=x
,y=x
,y=x3在(0,+∞)上是增函数,得到④正确.
根据含量词的命题的否定规则判定出②不正确;
通过构造函数,根据导函数的正负与函数单调性的关系求出y=10x-x2>1,进一步能判定出③正确;
根据5个常见幂函数的图象得到函数y=x-1在(0,+∞)上是函减数;函数y=x
| 1 |
| 2 |
| 1 |
| 3 |
解答:解:对于①,△ABC中,因为“A>B”?a>b?2RsinA>2RsinB?sinA>sinB,
所以①△ABC中,“A>B”是“sinA>sinB”的充要条件,
所以①正确;
对于②,若命题p:?x∈R,sinx≤1,则?p:?x∈R,sinx>1;
所以②不正确;
对于③,令y=10x-x2,y′=10xln10-2x,y″=10xln10ln10-2,
所以y″>0,所以y′=10xln10-2x在(0,+∞)上是增函数
所以y′>0,所以y=10x-x2在(0,+∞)上是增函数,所以y=10x-x2>1,所以10x>x2在(0,+∞)上恒成立
所以③正确
对于④,函数y=x-1在(0,+∞)上是函减数;函数y=x
,y=x
,y=x3在(0,+∞)上是增函数
所以④正确.
函数y=x-1在(0,+∞)上是函减数;函数y=x
,y=x
,y=x3在(0,+∞)上是增函数
故选C.
所以①△ABC中,“A>B”是“sinA>sinB”的充要条件,
所以①正确;
对于②,若命题p:?x∈R,sinx≤1,则?p:?x∈R,sinx>1;
所以②不正确;
对于③,令y=10x-x2,y′=10xln10-2x,y″=10xln10ln10-2,
所以y″>0,所以y′=10xln10-2x在(0,+∞)上是增函数
所以y′>0,所以y=10x-x2在(0,+∞)上是增函数,所以y=10x-x2>1,所以10x>x2在(0,+∞)上恒成立
所以③正确
对于④,函数y=x-1在(0,+∞)上是函减数;函数y=x
| 1 |
| 2 |
| 1 |
| 3 |
所以④正确.
函数y=x-1在(0,+∞)上是函减数;函数y=x
| 1 |
| 2 |
| 1 |
| 3 |
故选C.
点评:本题考查三角形的正弦定理;含量词的命题的否定规则:量词交换,结论否定;导函数的正负与函数单调性的关系:导函数为负函数单减,导函数为正函数单增,是一道综合题.

练习册系列答案
相关题目
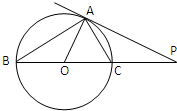 (2012•汕头一模)(几何证明选讲选做题)已知PA是⊙O的切线,切点为A,直线PO交⊙O于B、C两点,AC=2,∠PAB=120°,则⊙O的面积为
(2012•汕头一模)(几何证明选讲选做题)已知PA是⊙O的切线,切点为A,直线PO交⊙O于B、C两点,AC=2,∠PAB=120°,则⊙O的面积为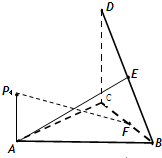 (2012•汕头一模)如图,直角△BCD所在的平面垂直于正△ABC所在的平面,PA⊥平面ABC,DC=BC=2PA,E为DB的中点.
(2012•汕头一模)如图,直角△BCD所在的平面垂直于正△ABC所在的平面,PA⊥平面ABC,DC=BC=2PA,E为DB的中点.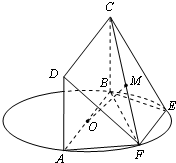 (2012•汕头一模)如图,AB为圆O的直径,点E、F在圆O上,AB∥EF,矩形ABCD所在的平面和圆O所在的平面互相垂直,且AB=2,AD=EF=1.
(2012•汕头一模)如图,AB为圆O的直径,点E、F在圆O上,AB∥EF,矩形ABCD所在的平面和圆O所在的平面互相垂直,且AB=2,AD=EF=1.